Misère Connect Four

It is well known that it is impossible to win at noughts and crosses (tic-tac-toe) unless your opponent makes a mistake, because if both players play optimally, the result is a tie. It is also true, but much harder to prove, that the game of draughts (checkers) is a tie, meaning that neither player can force a win if both players play optimally. In 1988, James D. Allen and (independently) Victor Allis solved the game of Connect Four by proving that the game is a win for the first player, if both players play optimally.

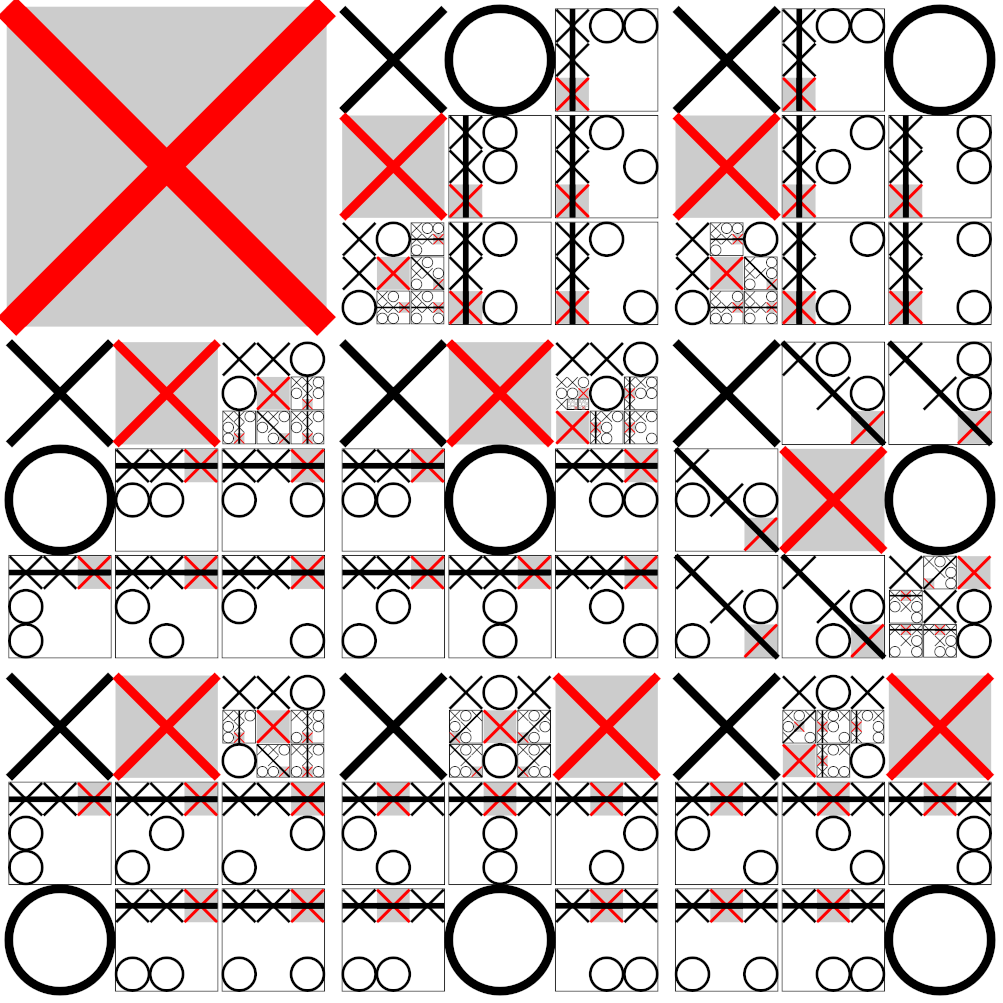
There are different levels at which a game can be “solved”. An ultra-weak solution to a game simply determines whether a player will win, lose, or draw if both players play optimally from the beginning, but it does not provide a method to accomplish this. A weak solution provides an optimal strategy for one player, starting with the first move, no matter what moves the opponent plays in reply. The diagram below shows an example of a weak solution to noughts and crosses if player X plays first; in particular, the best first move is to play in a corner. The aforementioned solutions to Connect Four by Allen and Allis are both “weak” solutions.

A strong solution to a game provides an optimal method for both players starting from any legal game configuration. A strong solution to Connect Four was described by John Tromp around 1995. The problem of finding a strong solution to a game is complicated by the fact that it can be difficult to identify legal configurations. For example, the picture below appears to depict a tie in a game of Connect Four, because neither player has managed to form four of their tokens into a line. However, as Victor Allis explained in his 1988 Master’s Thesis, it is impossible to reach this particular configuration by playing legal moves starting from an empty board.

In the misère version of a game, the winner is the player who would lose according to the usual rules. For example, in the game of misère Connect Four, players take turns dropping their tokens into the columns of a rectangular frame, just as in the ordinary version of the game. The difference is that to win a game of misère Connect Four, you need to force your opponent to create a row, column, or diagonal sequence of four of their own tokens. The recent paper Misère Connect Four is Solved by Robert Steele and Daniel B. Larremore gives a weak solution to misère Connect Four, proving that the game is a win for the second player on a standard 6 by 7 board. Even better, the solution has a simple description: Player 2 will win by always playing into an even numbered row, where the bottom row is row 1, and the top row is row 6. 

The picture above shows a partially played game according to this strategy, with Player 1 being Yellow and Player 2 being Red. Because Red is playing according to the “even numbered row” strategy, all the yellow tokens end up in odd rows, and all the red tokens end up in even rows. Because the number of rows is even and Yellow plays first, eventually Yellow will be forced to complete a row of four yellow tokens in the bottom row, thus losing the game according to the misère rules. A similar argument proves that Player 2 will win misère Connect Four on any board of even height, provided that there are at least four columns.

The paper goes on to solve misère Connect k on a board of width w and height h, where the standard game is the special case k=4, w=7, and h=6. The results are summarized in the table above. If the board has infinite width, or infinite height, or the board is too narrow to make a horizontal row of k tokens, the authors prove that the result will be a draw with optimal play.

One might expect the misère game not to be very interesting if the board has only one row and/or the game ends as soon as two consecutive tokens have the same colour. Surprisingly, this turns out not to be the case, and a fair amount of the paper is devoted to the analysis of these situations. A tied game of misère Connect 2 on a board with w=7 and h=1 necessarily consists of an alternating sequence of red and yellow tokens, like in the picture above. As soon as the first token is played on a board with one row, there is therefore only one possible way that the game can end in a draw. Despite this constraint, the optimal strategy still turns out to be surprisingly intricate. Misère Connect 2 on a board with one row turns out to be a draw if the board has width 1, 2, 4, or 6, and a win for Player 2 otherwise.

---

Picture credits and relevant links

The picture of Connect Four is by Popperipopp, the photo of the draughts board is by Jud McCranie, and the diagram of noughts and crosses strategies is by nneonneo. All three pictures appear on Wikipedia. 

The example game of noughts and crosses is a screenshot of Google’s version of the game.

The table of misère Connect k outcomes appears in the paper by Robert Steele and Daniel B. Larremore.

The other graphics are my own work.

John Tromp has a GitHub page with many interesting Connect Four resources. 

Substack management by Buzz & Hum.