Wallpaper groups and interlocking assemblies
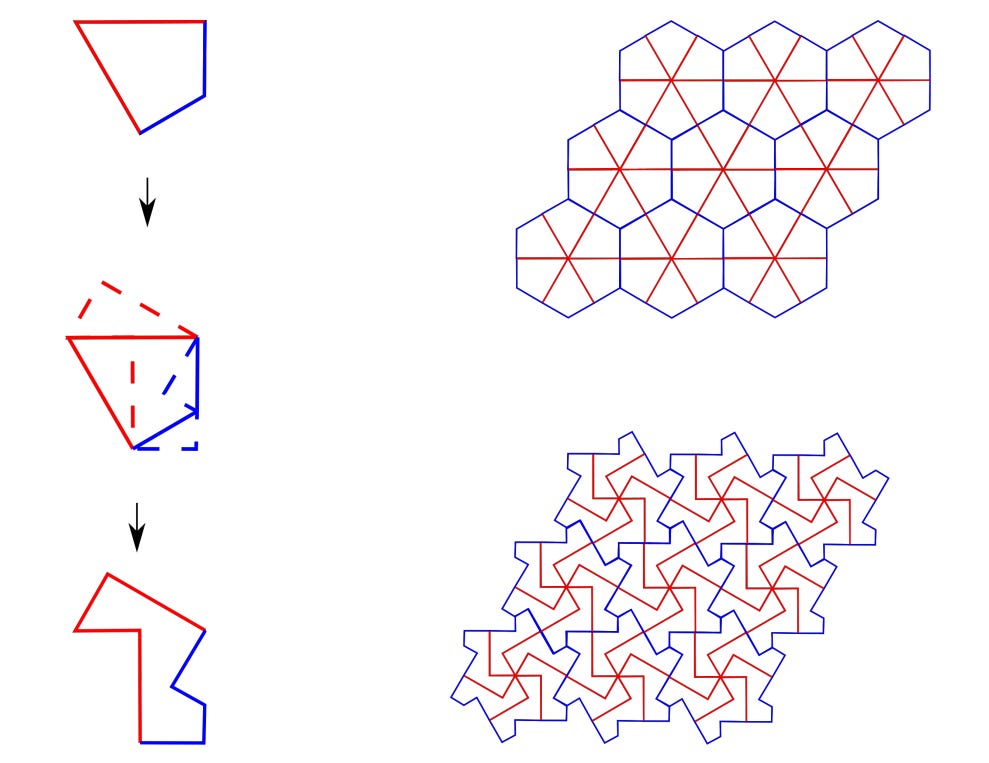
The patterns in the picture above illustrate an example of a wallpaper group, which is a two-dimensional repeating pattern with a particular kind of symmetry. The pattern has translational symmetry in two independent directions, as well as rotational symmetries of various kinds. It is invariant under rotation by a multiple of 60° about the middle of one of the hexagons, or under rotation by a multiple of 120° about the middle of one of the triangles. It is also invariant under rotation by a multiple of 180° about the middle of one of the line segments shared by two adjacent triangles. All the other symmetries are combinations of these ones; in particular, there is no reflectional symmetry in the pattern.
It is a theorem that there are exactly 17 essentially different wallpaper groups, and the symmetries of each one have a description like the one in the previous paragraph. Some of the wallpaper groups have some reflectional symmetry, and others have glide symmetry. The above picture of footprints is a good example of glide symmetry. Although it has no line of mirror symmetry, the picture is symmetric under reflection in the horizontal axis combined with a suitable horizontal shift.
The work of the artist M.C. Escher sometimes features repeating two-dimensional patterns that morph from one form into another. An example of this appears in his 1938 picture Sky and Water I, shown above. The recent paper Constructing Interlocking Assemblies with Crystallographic Symmetries by Tom Goertzen calls this phenomenon the Escher trick, and gives it a formal definition in the paper.
In the picture above, the Escher trick is used to morph a tiling of the plane by kite shapes into a tiling of the plane by irregular 8-sided shapes, in such a way that the tiles appearing in the intermediate stages are all polygons. Each of these intermediate tilings has all the same rotational and translational symmetries as the particular wallpaper group described in the first paragraph. The tiling by kite shapes has some additional reflectional symmetry, but this can be ignored.
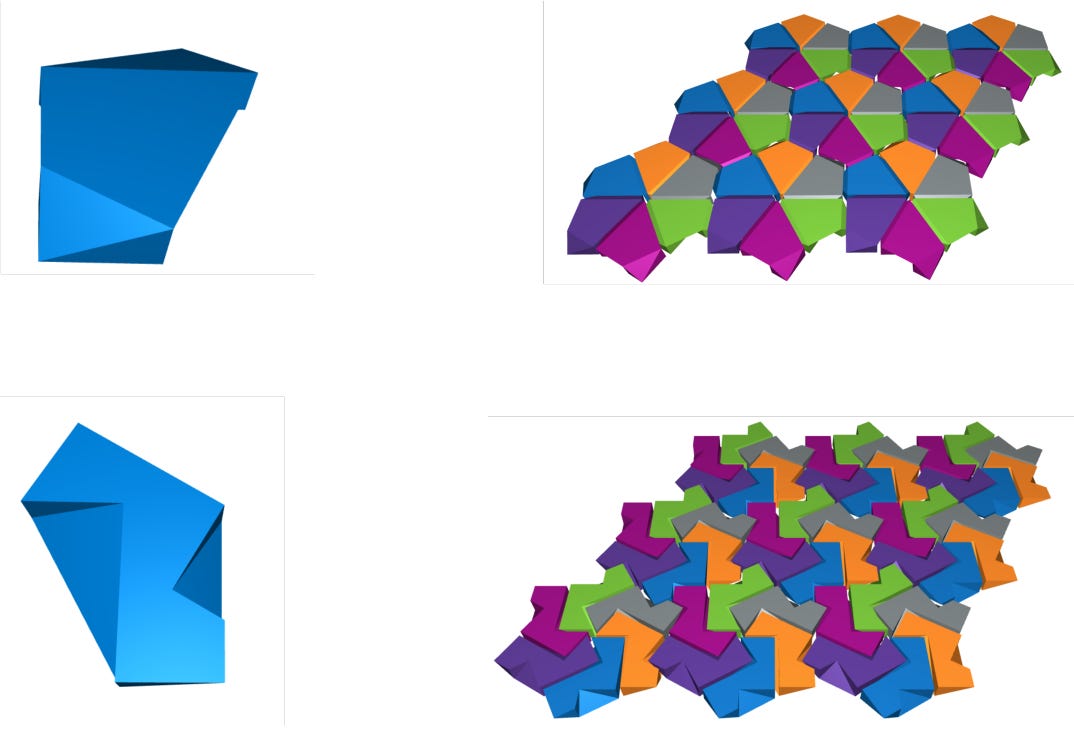
The morphing tile can be used to construct the layers of the three dimensional blue block shown above. Its top surface is the shape of the kite tile, and its bottom surface has the shape of the irregular octagon. These tiles fit neatly together into the flat surface shown above. One side of this surface looks like the tiling of the plane by kite shapes, and the opposite side of the surface looks like the tiling of the plane by irregular octagons.
The resulting tiled surface has a remarkable property: it is what the paper calls an interlocking assembly. What this means is that if the blocks in certain key positions, called the frame, are held fixed, then all the other blocks will be locked into position, without the need for any adhesive. This is a desirable property from the point of view of engineering, because it means that broken pieces in the structure can be replaced relatively easily.
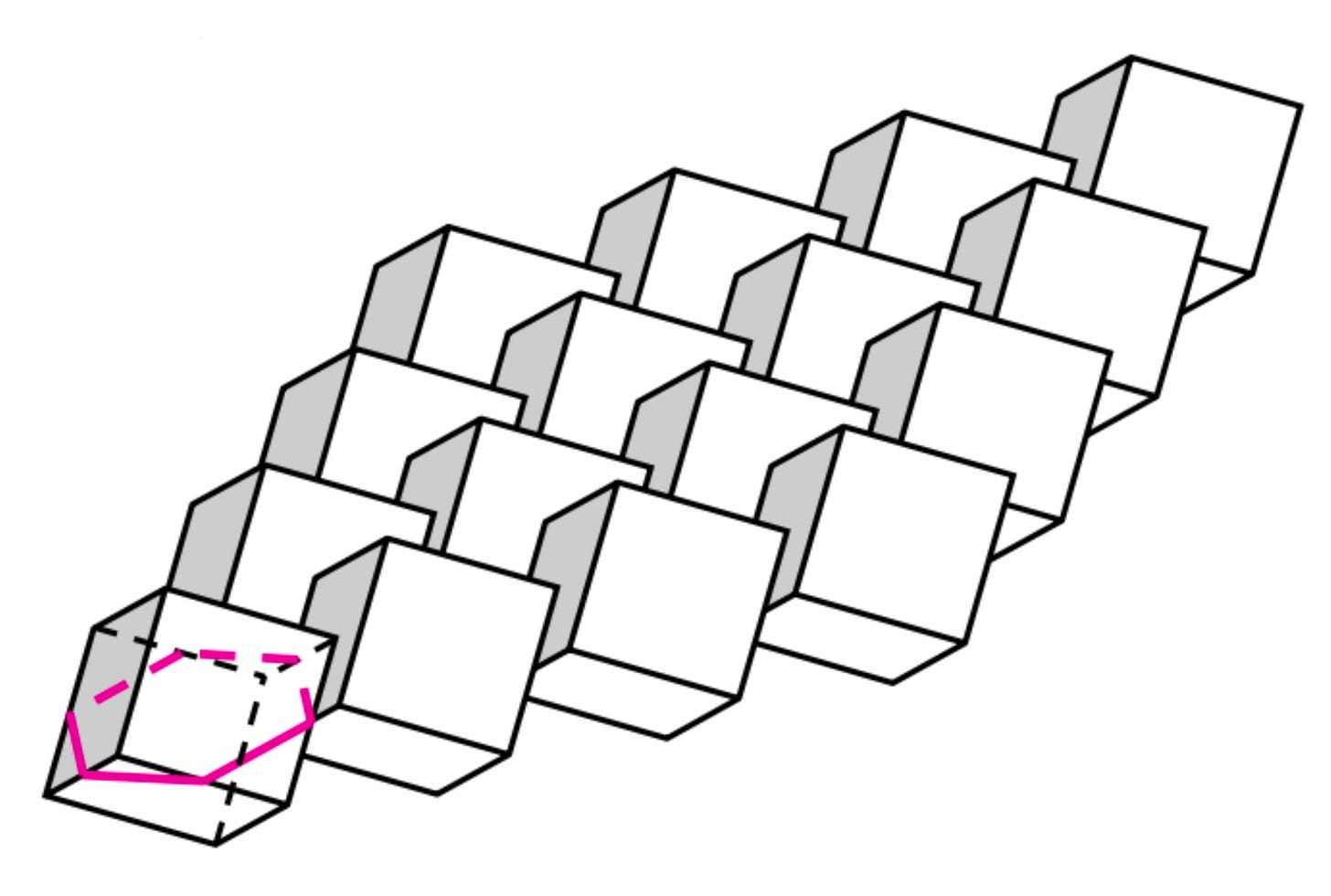
Compare this to what happens in the children’s game Don’t Break the Ice, shown above. The game begins by making a stable flat surface of cubes that are held in place by pressure either from adjacent cubes, or from the surrounding frame. During play, these cubes can be dislodged from the surface by applying a vertical force without damaging the cubes. In an interlocking assembly, this would be impossible: if the blocks in the frame are fixed, then it is impossible to dislodge any of the other blocks without damaging them.
The picture above comes from the 2003 paper Topological Interlocking of Platonic Solids: A Way to New Materials and Structures by Arcady V. Dyskin, Yuri Estrin, A.J. Kanel-Belov, and E. Pasternak. It shows a way to interlock cubes in a stable arrangement, and something similar can be done with regular tetrahedra and octahedra. A disadvantage of this construction relative to the new construction described above is that it does not produce a surface with a flat top and a flat bottom.
The paper by Tom Goertzen contains many other constructions along these lines, including examples of blocks with smooth edges. One of these is shown in the above picture, from the front, the side, and the top.
Picture credits and relevant links
The picture of the polygonal tiling is by Arthur Baelde, the picture of the Persian ornament is in the public domain, and the picture of the footprints is by Poznaniak. All three pictures appear on the Wikipedia page on wallpaper groups.
The 1938 picture Sky and Water I is by M.C. Escher.
The picture of the game Don’t Break the Ice is from SoSickWithIt on Etsy, in case you would like to buy the game.
The other graphics (apart from the one showing the interlocking cubes) are from the paper by Tom Goertzen.
Substack management by Buzz & Hum.







Excellent post! I like the way it is related to actual wallpaper designs and also the game!