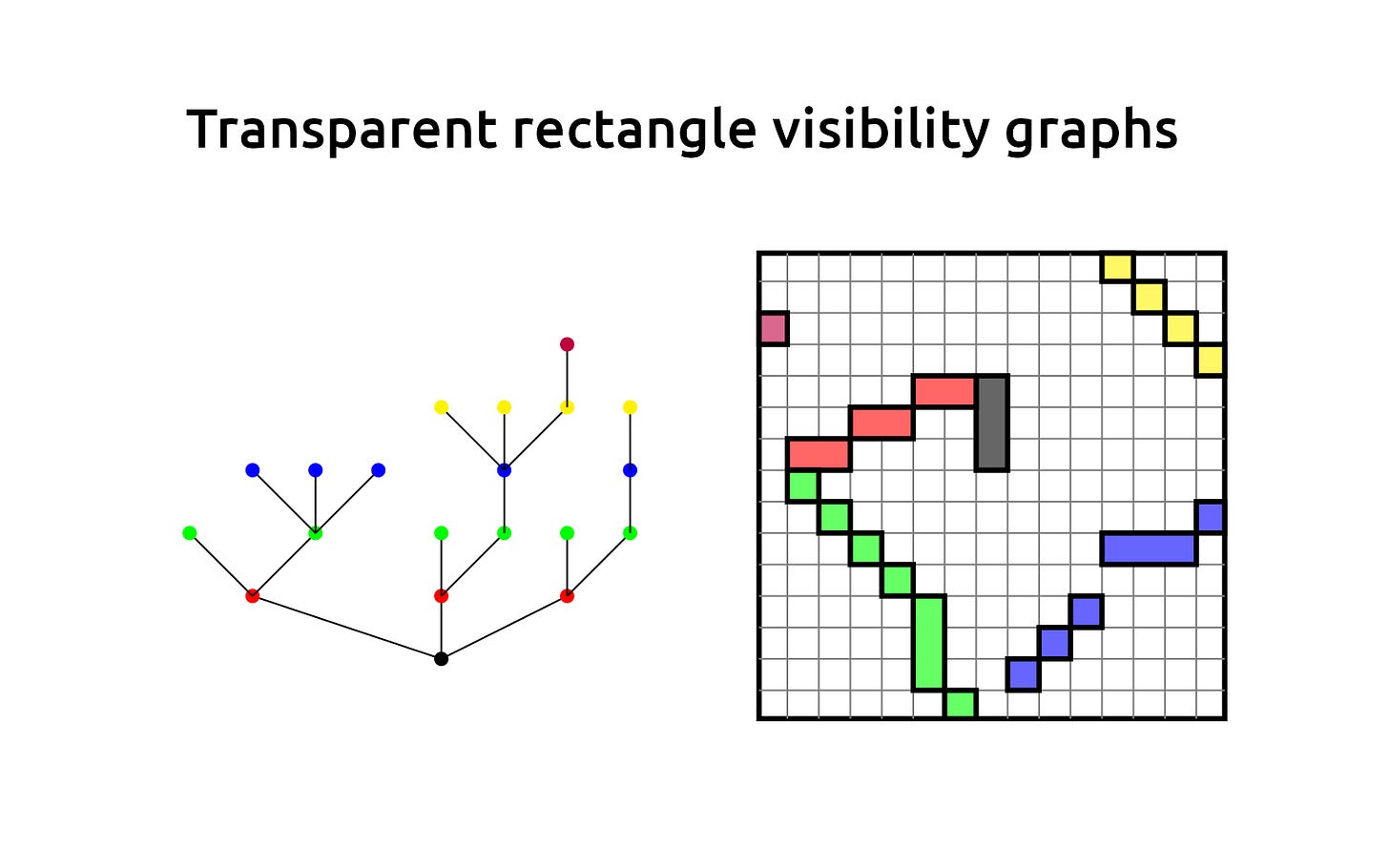
Transparent rectangle visibility graphs
A graph consists of a set of vertices, some of which are joined in pairs by edges. It is possible to reconstruct the graph shown above and to the left from the arrangement of rectangles shown on the right. Each of the 20 rectangles corresponds to one of the 20 vertices in the graph, and there is an edge between two vertices if and only if there is a dir…
Keep reading with a 7-day free trial
Subscribe to A Piece of the Pi: mathematics explained to keep reading this post and get 7 days of free access to the full post archives.