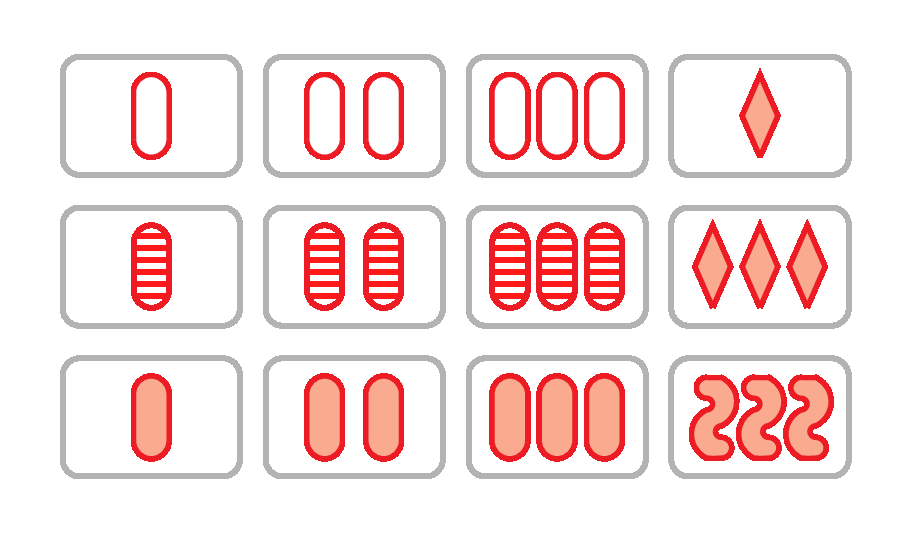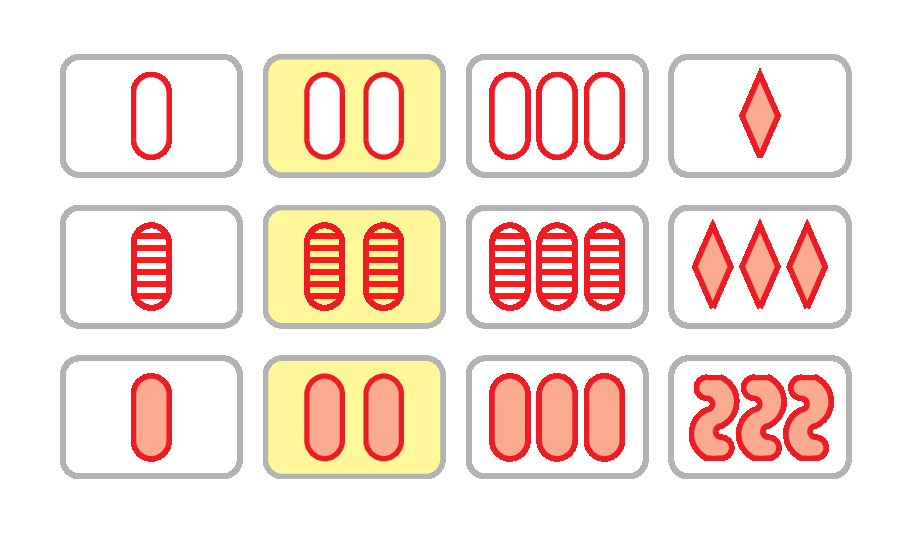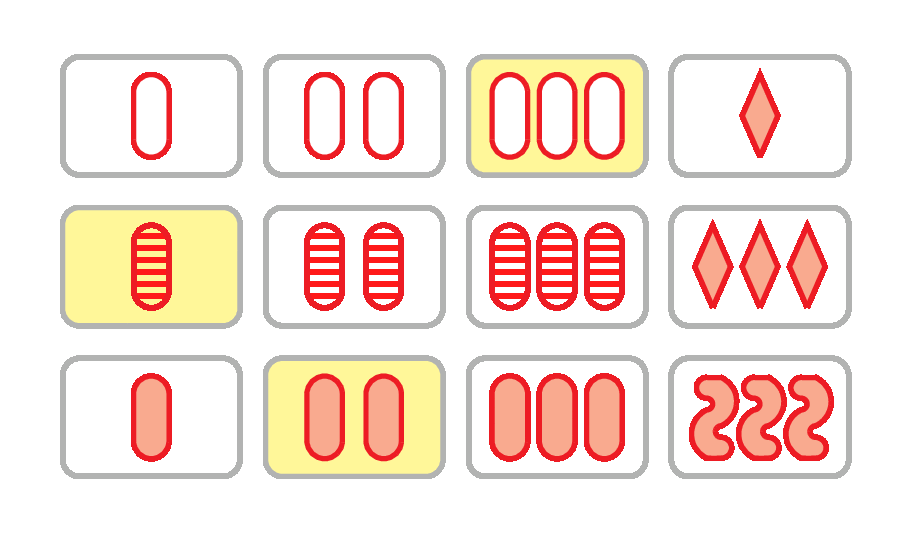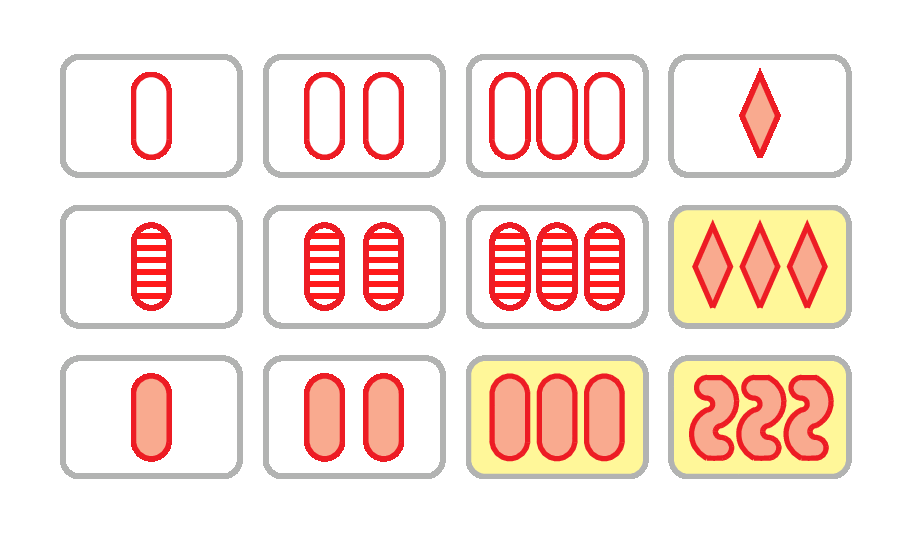
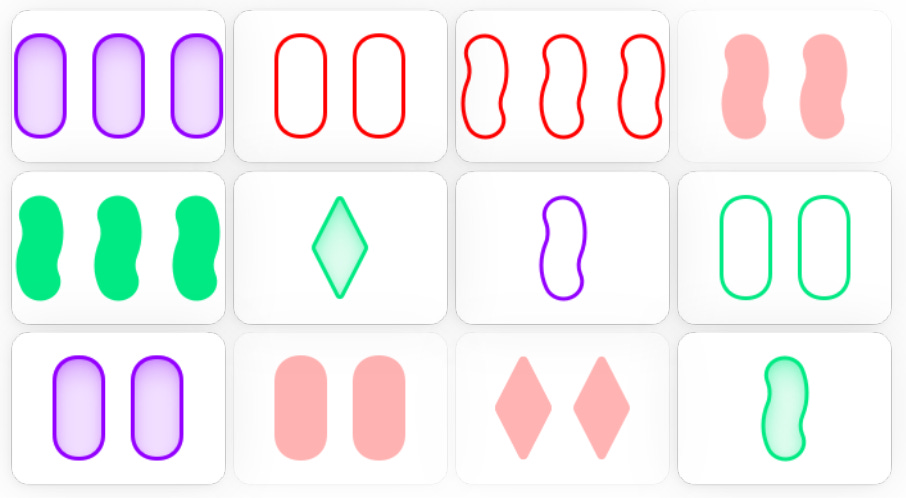
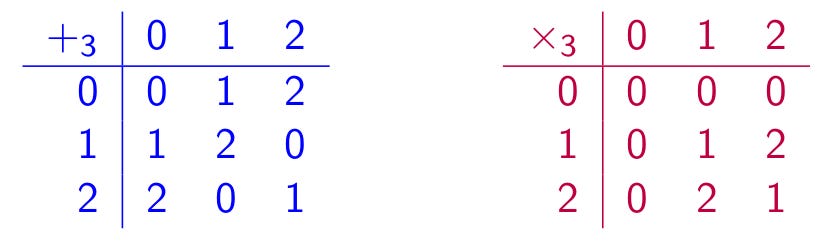The maximum number of SETs for 12 cards
SET is a card game that is played with a deck of 81 cards. The shape(s) shown on each card have four qualities: quantity, shading, colour, and shape. Each of the qualities can have one of three possible values: the quantity can be one, two, or three; the shading can be open, striped/shaded, or solid; the colour can be red, green, or purple; and the shape can be diamond, oval, or squiggle. A “set” is a collection of three cards, each quality of which is either “all the same” or “all different”, and the goal of the game is to identify as many sets as possible. For example, the three green cards in the middle row of the grid below (one striped green diamond, two open green ovals, three solid green squiggles) form a set, because the cards have all different quantities, all different shadings, all the same colour, and all different shapes.
The game SET is mathematically interesting because it can be understood using linear algebra, which is the study of vector addition, scalar multiplication, and vector spaces. In many applications, the scalars are the real numbers or the complex numbers, but in the case of the game SET, the set of scalars is the field with three elements, F3. We can think of these as the numbers 0, 1, and 2 under the operations of addition and multiplication modulo 3, as shown in the tables below.
It follows from the tables that 0+0+0=0, 1+1+1=0, 2+2+2=0, and 0+1+2=0. In fact, if a, b, and c are elements of the field F3 with the property that a+b+c = 0, then it must be the case that either a, b, and c are all the same, or that a, b, and c are all different. This is the property that makes F3 so useful for understanding the game SET. Each of the 81 cards can be encoded as a sequence (x, y, z, w) of elements from F3, where the x encodes the quantity, the y encodes the shading, the z encodes the colour, and the w encodes the shape, according to the rules in the table below.
With this encoding, “one striped green diamond” corresponds to the sequence (0, 1, 1, 0), “two open green ovals” corresponds to (1, 0, 1, 1), and “three solid green squiggles” corresponds to (2, 2, 1, 2). If we add these sequences up modulo 3, we find that (0, 1, 1, 0) + (1, 0, 1, 1) + (2, 2, 1, 2) = (0, 0, 0, 0). The key observation is that three cards form a set if and only if their corresponding vectors add up to zero. From an algebraic point of view, the game of SET is a four dimensional vector space over F3, and the goal is to find three points that lie on a line. The designers of the game found a way to express this in a way that is palatable to non-mathematicians, but linear algebra is still useful in understanding what is going on.
The recent paper The Maximum Number of Sets for 12 Cards is 14 by Justin Stevens and Duncan Wilson gives a human-readable proof of the result in the title. It is relatively straightforward to construct a set of 12 cards that contains 14 different sets, as shown above and in the top animation. Remarkably, it is even possible to do this using only red cards. It is slightly harder to prove that it is impossible to find a set of 12 cards containing 15 different sets, but the authors do that as well. The paper also gives human-readable proofs of analogous results for 11 or fewer cards.
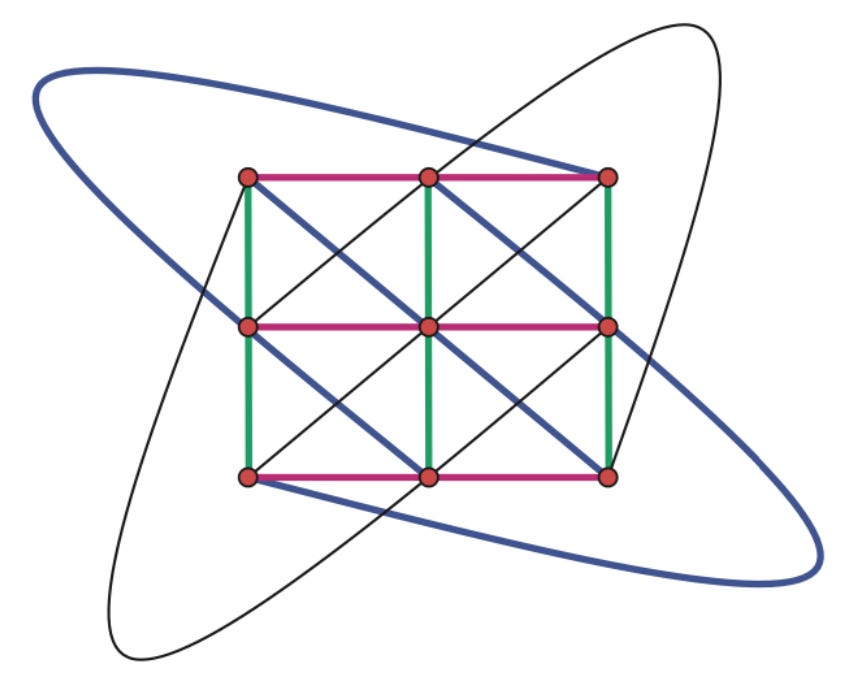
The case of 9 cards is particularly interesting. From the point of view of linear algebra, we can select 9 cards that form a 2-dimensional subspace of the 4-dimensional vector space, and this ensures that any two of the 9 cards lie on a line with one of the other 7 points. This produces an arrangement of 9 points and 12 lines as shown above, which the paper calls a magic square. It follows that there exists a set of 9 cards containing 12 sets, but no set of 9 cards containing 13 sets. Another way to construct this magic square is to ignore the rightmost column of the animation above; these 9 cards and the 12 sets containing them give the magic square.
The case of 27 cards is also easy, because 27 is the size of a 3-dimensional subspace of a 4-dimensional vector space. This enables us to find a set of 27 cards, any two of which form a set with one of the other 25 cards. A counting argument then shows that the number of sets formed in this way is 117=27×26/6. The paper also makes some progress on computational techniques giving bounds on the maximum sets for numbers of cards between 13 and 26.
Picture credits and relevant links
The tables are my own work. The animation is my own work but is based on the setdeck graphics package by Gwyneth Whieldon.
The other graphics come from the paper by Justin Stevens and Duncan Wilson.
I thank Annabel Green for some helpful conversations.
Substack management by Buzz & Hum.