Partitions and primes
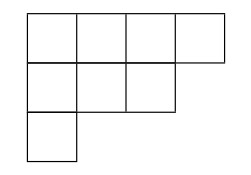
The picture above shows all the partitions of the numbers 1 up to 8. For example, the partitions of 4 are the sequences of weakly decreasing positive integers that add up to 4. There are five ways to do this: 4, 3+1, 2+2, 2+1+1, and 1+1+1+1. Each of these five partitions corresponds to a way to attach 4 squares edge-to-edge to make the shape of a tetris piece. The numbers being added up correspond to the number of squares in each row of the shape. For example, the shape below has 4 squares in the first row, 3 in the second, and 1 in the third, so it corresponds to the partition of 8 given by 4+3+1.
Partitions show up in a lot of areas of mathematics, so it is desirable to have a way to count them. Counting the shapes in the top picture shows that the number of partitions of 1, 2, 3, 4, 5, 6, 7, and 8 is equal to 1, 2, 3, 5, 7, 11, 15, and 22 respectively. It would be nice to have a general formula for p(n) (the number of partitions of n) involving binomial coefficients or something, but no such formula is known.
The formula above is a fairly simple generating function for the numbers p(n), but it involves an infinite product and it is not a very helpful way to calculate the individual numbers.
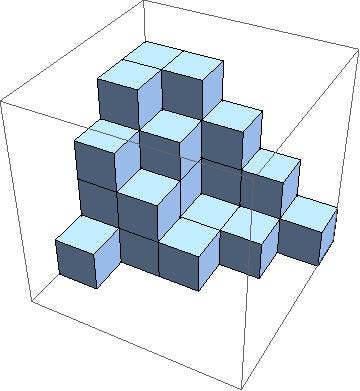
The picture above is an example of a plane partition, which is a kind of 3-dimensional analogue of the integer partitions mentioned earlier. Instead of placing squares flush into the corner of a rectangle, we now imagine stacking cubes flush into the corner of a room. The picture shows a plane partition of 30, meaning that there are 30 boxes involved in the stack.
Another way to think about this is to imagine viewing the box stack from above, and then recording the heights of each stack of boxes. This results in a partial array of numbers that adds up to 30, as above. The number PL(n) of plane partitions of n for n=1, 2, 3, 4, 5, 6, 7, 8 turns out to be 1, 3, 6, 13, 24, 48, 86, and 160 respectively. As in the case of integer partitions, there is not a good formula for the number of plane partitions of n, but there is a nice generating function, shown below.
The generating function for plane partitions was discovered by P.A. MacMahon (1854–1929). As well as being a major in the British Army, MacMahon (pictured below) essentially invented the area of mathematics now known as algebraic combinatorics, which he called combinatory analysis.
A Diophantine equation is a polynomial equation with integer coefficients, in which only integer solutions are of interest. A famous example of a Diophantine equation is x2 + y2 = z2, whose integer solutions are Pythagorean triples, such as 32 + 42 = 52.
Another example of a Diophantine equation is x – (y + 1)(z +1)=0. This equation has the interesting property that it has a solution in positive integers if and only if x is composite. For example, 21 is a composite number, because 21=3×7. This corresponds to x=21, y=2, z=6 being a solution to the Diophantine equation, because 21 – (2+1)(6+1)=0.
In 1976, James P. Jones, Daihachiro Sato, Hideo Wada, and Douglas Wiens found an explicit Diophantine equation whose positive outputs from nonnegative integer inputs are precisely the prime numbers. Their solution, shown above, is a polynomial of degree 25 in 26 variables a, b, c, …, z.
The recent paper Integer partitions detect the primes by William Craig, Jan-Willem van Ittersum, and Ken Ono shows how to generate the prime numbers using Diophantine equations based on MacMahon’s work on partitions. More specifically, these equations involve certain integer sequences M1(n) and M2(n) defined in the formula below.
These integers M1(n) and M2(n), which were introduced by MacMahon, can also be defined directly in terms of partitions. Craig, van Ittersum, and Ono find infinitely many Diophantine equations in these MacMahon-style partition functions that detect primes. The simplest of these is the remarkably concise result that if n is positive, then (n2 – 3n + 2)M1(n) – 8M2(n) is always at least zero, and if n is at least 2, the expression evaluates to zero if and only if n is prime.
PIcture credits and relevant links
The picture of the integer partitions is by R.A. Nonenmacher and appears on Wikipedia.
The picture of the plane partition is by Sophie Hofmanninger and appears on Wikipedia.
The screenshot of the theorem by James P. Jones, Daihachiro Sato, Hideo Wada, and Douglas Wiens comes from their paper Diophantine representation of the set of prime numbers.
Wikipedia has an (inadequate) article on Percy Alexander MacMahon. The photograph of MacMahon appears on that page, but I do not know where it came from originally.
The other graphics are my own work.
The number of integer partitions of n and the number of plane partitions of n appear in the On-Line Encyclopedia of Integer Sequences.
My post on self complementary ideals also features plane partitions.
Substack management by Buzz & Hum.





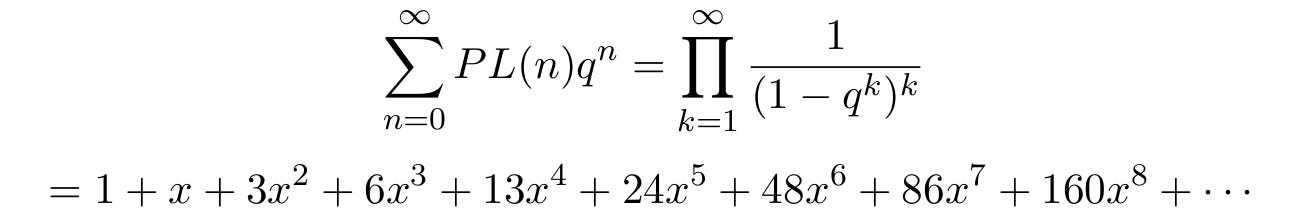

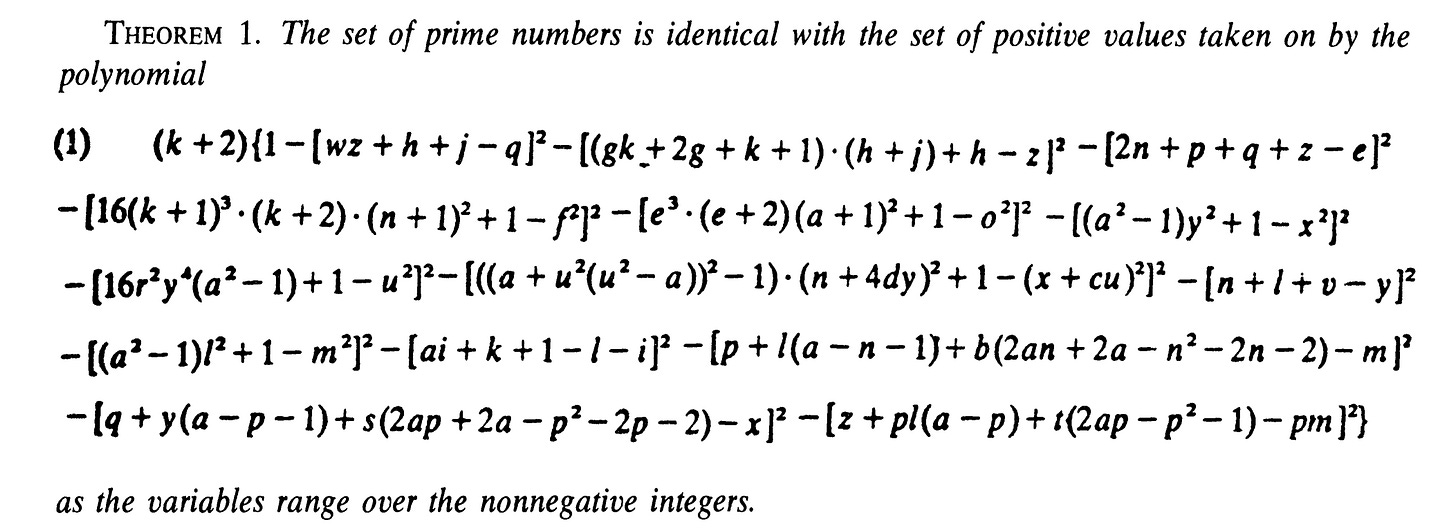

I edited the last paragraph of the post to reflect the fact that the authors found infinitely many Diophantine equations based on MacMahon's partition functions.