No three in a line
This picture shows how to place 20 points on the vertices of a 10×10 grid in such a way that no three of the points lie on a straight line. So what is the largest number of points that can be placed on an n×n grid without any three lying on a straight line? Is the answer 2n?
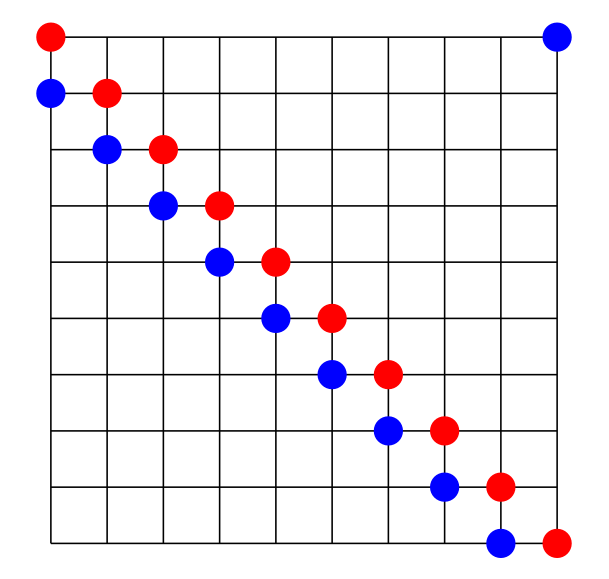
Because the grid contains only n rows, and each row can contain at most 2 of the points, it follows that it is impossible to place more than 2n points on an n×n grid without violating the “no three in a line” constraint. A similar remark applies to columns, and this explains why the 20 points on the 10×10 grid in the picture above have the property that each row and each column of the grid contains precisely two points. The picture below shows that it is easy to find arrangements of 2n points with the property that no row or column of the grid contains more than 2 points, but this particular arrangement is not a solution because many of the points lie on the same diagonal line.
It is not possible to place 2n points on an n×n grid if n=1, because a 1×1 grid only has one location to place a point, but solutions to the “no three in a line” problem are known for all 2≤n≤46. Furthermore, the number of different solutions for a given n can be quite large. For example, there are 152210 ways to place 36 points on an 18×18 grid with no three in a line. This might suggest that if n is a very large number, then it should easily be possible to place 2n points on an n×n grid with no three in a line. The question of whether or not this is always possible has been open since 1900, when Henry Dudeney posed the problem of placing 16 pawns on a chessboard with no three in a line (as shown below).
Given the abundance of solutions to the problem for small values of n, it is perhaps surprising that mathematicians expect the problem to have a negative answer in general. More precisely, it is conjectured that whenever n is large enough, it will be impossible to place 2n points on an n×n grid with no three in a line. Here, “large enough” is expected to mean something like “for all n bigger than about 600”.
Let us define f(n) to be the maximum number of points that can be placed on an n×n grid with no three in a line. Although the exact values of f(n) are not known, it follows from earlier reasoning that we have f(n)≤2n. In 1975, R.R. Hall, T.H. Jackson, A. Sudbery, and K. Wild proved that f(n) is greater than about 1.5n, and Richard K. Guy conjectured that for large values of n, we have f(n)≤1.814n. (The number 1.814 comes from π/√3.) If Guy’s conjecture is correct, then it follows that f(n)=2n will never hold if n is larger than a certain value, and therefore that it will be impossible to place 2n points on a grid with no three in a line. If n=600, we would expect to be able to place at least 900 points (900=1.5×600) on a 1200×1200 grid with no three in a line, but not as many as 1200. For very large values of n, we might only be able to place 1.814n points with no three in a line, which would miss the target of 2n points by a wide margin.
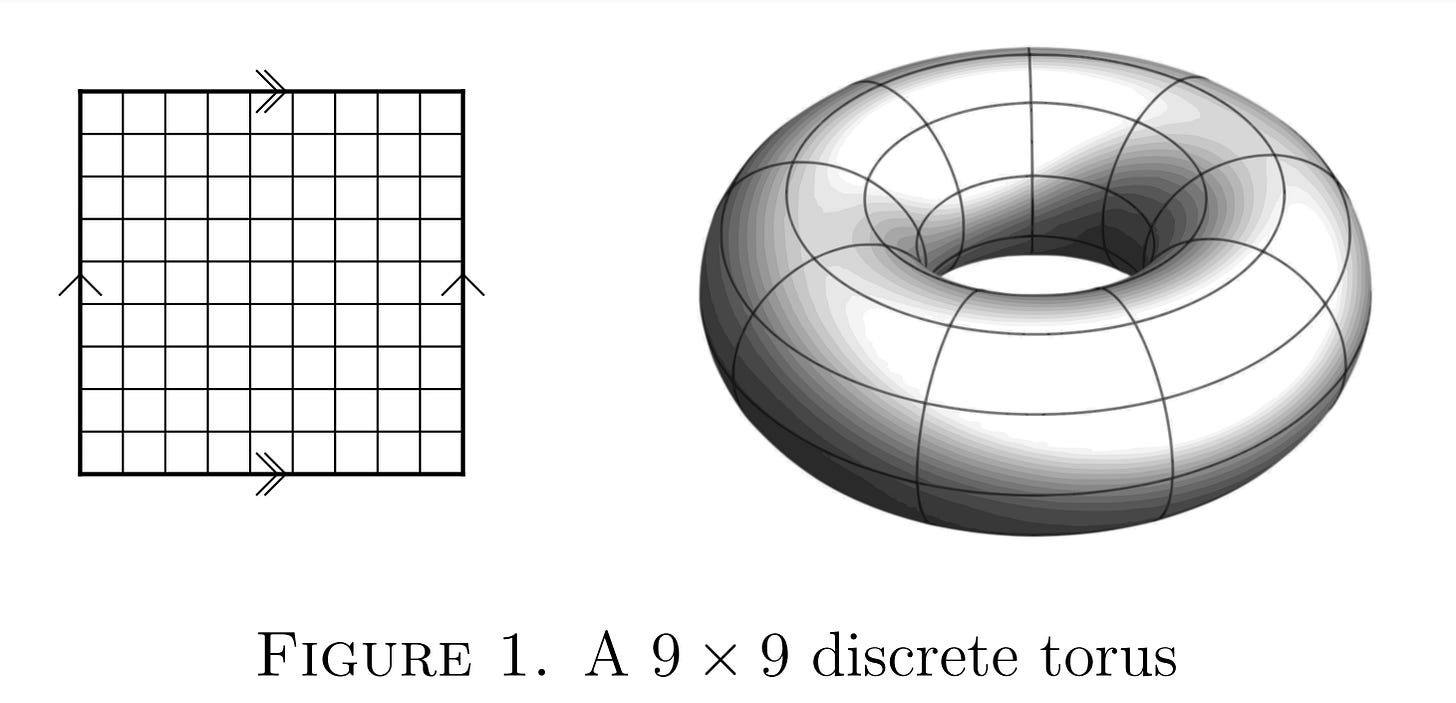
One can also pose a version of the three-in-a-line problem on the surface of a torus, as shown above. In this situation, the left and right edges of an m×n grid are identified with each other, and the top and bottom edges of the grid are identified with each other. The resulting shape is called an m×n discrete torus. (This phenomenon may be familiar from certain video games, where passing off the right edge of the screen makes a player reappear on the left edge.) When viewed as a subset of the grid, a “straight” line on the torus may cross the vertical and horizontal edges of the grid several times before meeting back up with itself, as in the diagram below.
Let us define T(m,n) to be the maximal number of points that can be placed on an m×n discrete torus with no three in a line, in the sense of the previous paragraph. Unlike the corresponding case of the grid, some precise information is known about the numbers T(m,n). For example, Jim Fowler, Andrew Groot, Deven Pandya, and Bart Snapp proved in 2012 (using a sophisticated geometric argument) that if p is an odd prime number then T(p,p)=p+1. In contrast, the values of f(p) for large p are not even known.
I found out about this topic from the recent paper No-Three-in-a-Θ: Variations on the No-Three-in-a-Line Problem by Natalie Dodson, Anant Godbole, Dashleen Gonzalez, Ryan Lynch, and Lani Southern. The authors obtain some bounds for the number of points that can be placed on an n×n grid without any three of them forming a particular angle of θ. The most interesting cases arise when tan(θ) is a rational number.
Picture credits and relevant links
Henry Dudeney (1857–1930) was well known as a creator of mathematical puzzles.
The number of ways of placing 2n points on an n×n grid with no three in a line is given by sequence A000755 in The On-Line Encyclopedia of Integer Sequences.
The chess graphic is by Cmglee and appears on Wikipedia’s page on the No-three-in-line problem. The page also gives some geometrical applications of the no three-in-line problem.
The graphic of the grid and torus is from the paper The no-three-in-line problem on a torus by Jim Fowler, Andrew Groot, Deven Pandya, and Bart Snapp.
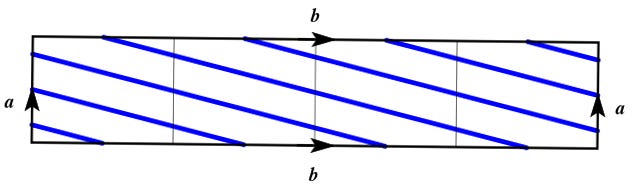
The graphic of the blue lines on the rectangle is by Volker Schatz and appears in Wikipedia’s entry on Torus knot.
The other graphics are my own work.
Substack management by Buzz & Hum.




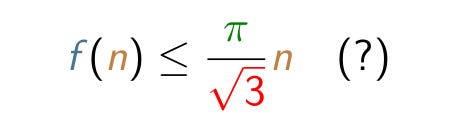
z3 is good for solve similar example
https://dev.to/taw/100-languages-speedrun-episode-23-ruby-z3-19b9
In my opinion setup 500x500 is possible resolve all solution for less than 2 day