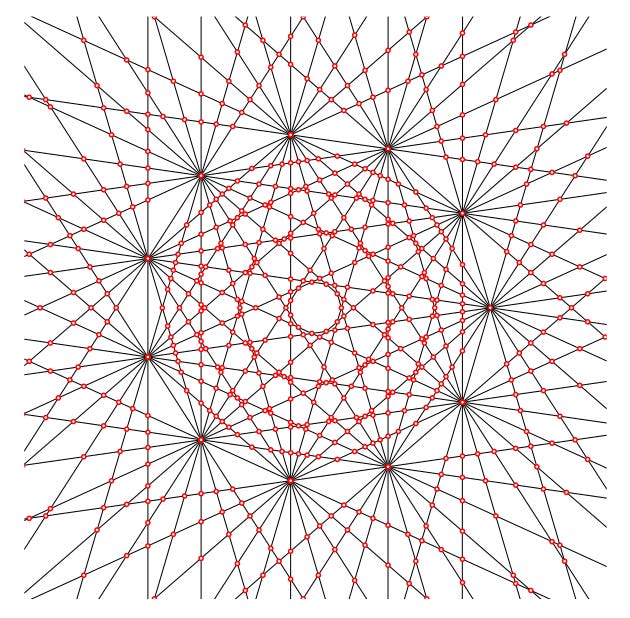
Intersections of chords of a circle
The picture above shows a regular polygon with 15 vertices, including all the diagonals between the 15 vertices, and all the intersections between the diagonals. These points of intersection, shown in red, are not distributed evenly throughout the shape, and they tend to be located away from the centre. In 1962, Jovan Karamata proved a formula that predicts what proportion of the red points lie within distance r from the origin as the number n of vertices tends to infinity.
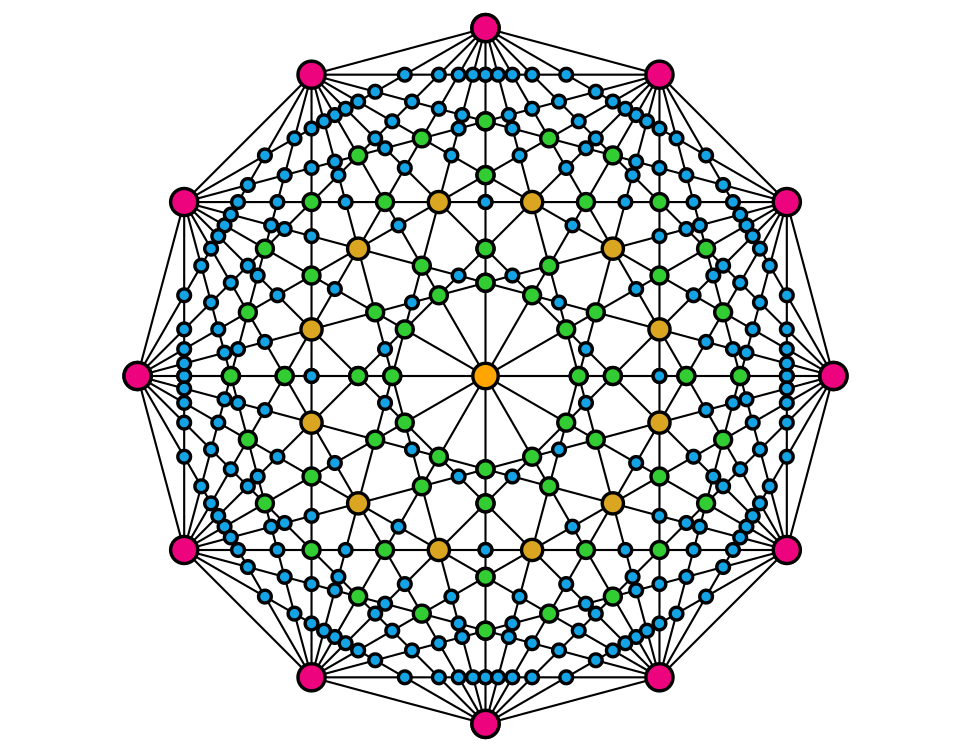
It is possible for more than two diagonals to intersect in the same point. For example, if the number n of vertices is even, then the central point of the shape will lie on the intersection of n/2 different diagonals. The picture above shows the situation for n=12, with the points of intersection colour-coded for multiplicity: the pink (respectively, yellow, brown, green, blue) points lie at the intersection of 11 (respectively, 6, 4, 3, 2) diagonals. Karamata’s Theorem takes these multiplicities into account, so that for example the point in the middle of the picture is weighted as if it were six different points with the same position.
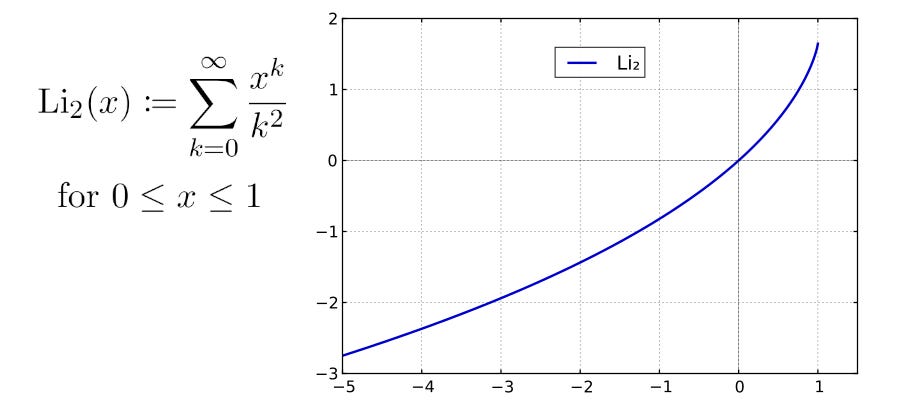
Unexpectedly, the key to understanding the density of the red points is Euler’s dilogarithm function, Li2(x), which is shown above. The function satisfies Li2(0)=0 and Li2(1)=π2/6 (or about 1.64). Karamata’s Theorem says that, as n tends to infinity, the proportion of red points that lie within distance r of the origin tends to 6Li2(r2)/π2.
We can also try to ask the analogous question about the points of intersection of random chords of a circle. (A chord of a circle is a straight line segment drawn between two of its points.) If we draw two random chords on the same circle, how close to the centre is their point of intersection likely to be?
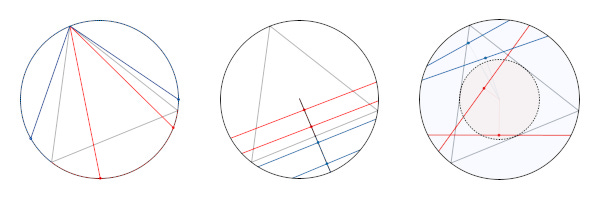
More importantly, what exactly do we mean by a “random” chord? Three possible definitions are shown above using a circle of radius 1 and an equilateral triangle inside it of side length √3. In the picture on the left, we choose two points uniformly at random on the circle and join them with a line segment. In the picture in the middle, we draw a radius of the circle in a random direction and choose a point uniformly at random on that radius. In the picture on the right, we choose a point uniformly at random inside the circle and construct a chord with that point as its midpoint. A chord is depicted as red if it is longer than √3, and blue if it is shorter than √3. Remarkably, the probability of a “random” chord being longer than √3 is ⅓ in the first case, ½ in the second case, and ¼ in the third case. This result is known as the Bertrand paradox.
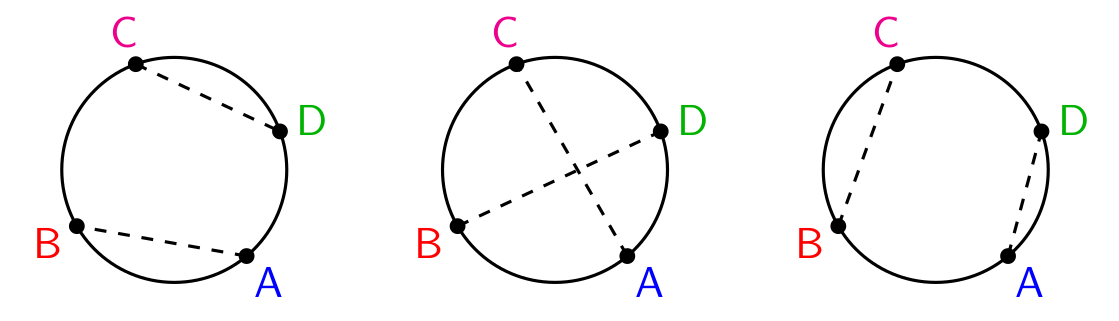
The recent paper Intersections of random chords of a circle by Cynthia Bortolotto and Victor Souza uses the first definition of “random chord”, where the chord is obtained by joining two randomly chosen points on the circumference. The main question addressed in the paper is: given two such random chords, what is the probability that their intersection lies within r of the centre? Given four points on a circle, there are three ways to join them together in pairs, as shown above, and only one of these three ways results in a point of intersection inside the circle. A natural guess as to the answer is one third of the number given by Karamata’s Theorem, namely 2Li2(r2)/π2, and indeed, this is what happens.
If we extend the chords to be complete lines rather than line segments, it is possible for the chords to intersect, but outside the circle, as in the picture above. The authors also give a formula to generalize Karamata’s Theorem to this case, but it is more complicated and does not involve the dilogarithm function.
Picture credits and relevant links
The graph of the dilogarithm function is by Geek3 and appears on Wikipedia.
The diagrams of the blue and red chords are by Robert Dodier and appear on the Wikipedia page about the Bertrand paradox.
The picture of the possible chords between four points on a circle is my own work.
The other pictures come from the paper by Cynthia Bortolotto and Victor Souza.
The Bertrand paradox is named after Joseph Bertrand (1822–1900). Bertrand has two other paradoxes named after him, one in economics, and another one in probability. None of these should be confused with Russell’s paradox, which is named after Bertrand Russell (1872–1970).
Substack management by Buzz & Hum.



Very interesting! Has this analysis been extended to higher dimensions?