How many triangles are there?
A well-known type of brain teaser invites the reader to count the number of triangles formed by dividing up a larger triangle using straight lines. In the example above, it appears that the answer is 16. But how do we know that we haven’t missed any?
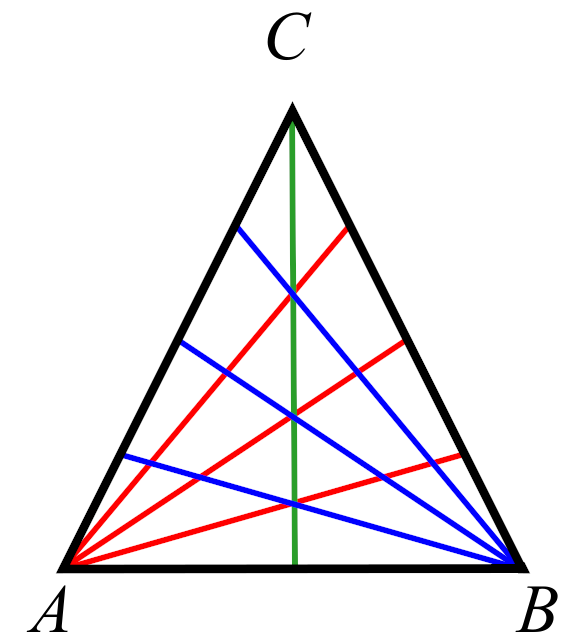
The recent paper Counting Triangles in Triangles by Jim Propp and Adam Propp-Gubin gives a formula for the number of triangles formed by dividing up a larger triangle ABC using cevians. A cevian is a straight line connecting a corner of the triangle to a point on the opposite edge. We define a, b, and c to be the numbers of cevians emerging from points A, B, and C respectively. For example, the picture above shows the case where a=3, b=3, and c=1.
It turns out that the number of triangles can be expressed in terms of binomial coefficients involving the numbers a, b, and c, as shown above. This formula has been stated without proof in other places, but what is nice about the paper is that the authors explain in detail why the formula works.
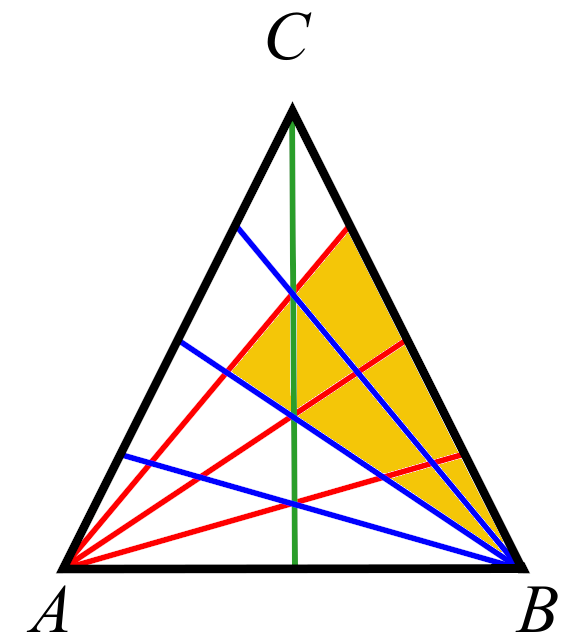
The key observation is that each of the triangles being counted is bounded by three straight lines. Each of these straight lines is either part of a cevian, or part of one of the edges of the big triangle. For example, the shaded triangle in the figure above is bounded by (1) the edge BC, (2) the uppermost red cevian, and (3) the middle blue cevian. Furthermore, this set of three lines defines a unique triangle.
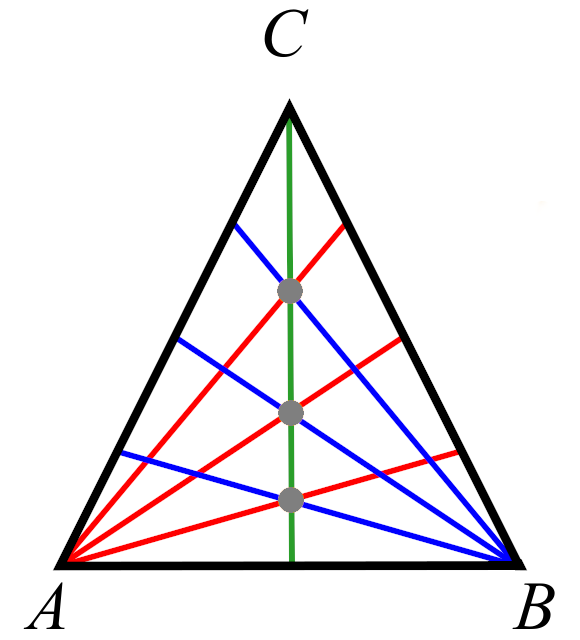
Some combinations of three lines do not define a triangle because they all meet at a point. This point may be one of the three corners of the triangle, or it may be one of the internal points of the triangle as indicated by the grey spots in the picture above. The number d in the formula is defined to be the number of these grey spots, and in our example, we have d=3. A case by case check shows that any three lines that do not meet at a common point will define a unique triangle.
How many ways can we choose three lines that intersect at the point A? There is a total of a+2 lines emerging from A: the a cevians, and the two edges AB and AC. The number of ways of choosing 3 objects from a total of a+2 is given by the binomial coefficient “(a+2) choose 3”, as defined above. There are similar formulas for the number of ways that three lines can meet at B or at C.
To count the total number of triangles, we start by counting the number of ways to select the three bounding lines. The total number of lines in the picture is a+b+c+3, because we need to count the three edges of the big triangle as well as all the cevians. The number of ways to select three of these lines is the first term of the formula, “(a+b+c+3) choose 3”. We then need to subtract all the collections of three lines that can meet at a point. This explains the other four terms in the formula, because three such lines can either meet at A, or at B, or at C, or at one of the internal points of the triangle. In the example at the top, a, b, c, and d are all equal to 1, and the formula above confirms that the total number of triangles is 16.
It is left as an exercise for the reader to show that the total number of triangles in the more complicated example is 96.
Picture credits and relevant links
The pictures of triangles are edited versions of the pictures in the paper by Jim Propp and Adam Propp-Gubin. The other graphics are my own work.
Cevians are named after Giovanni Ceva (1647–1734).
Substack management by Buzz & Hum.



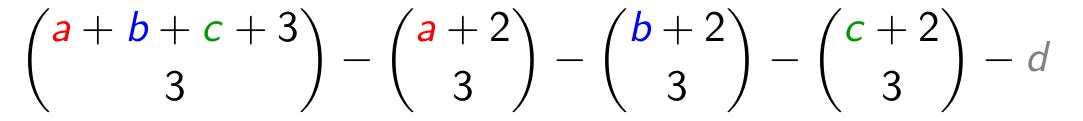
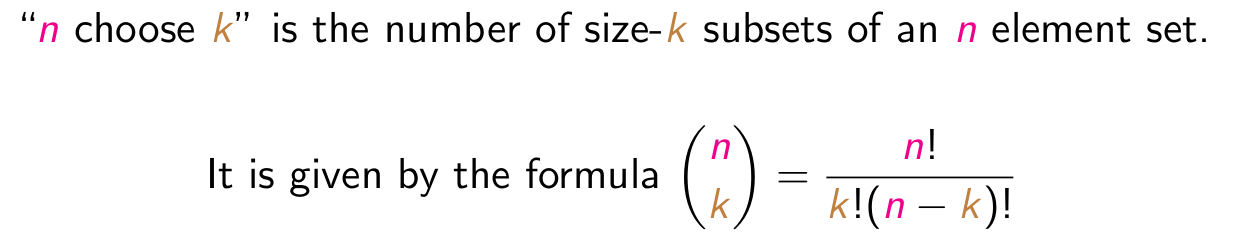
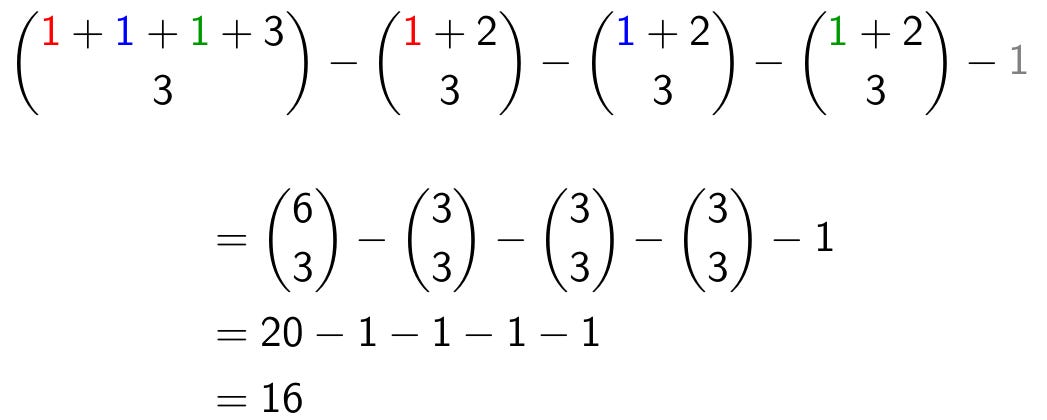
Nice summary! Your readers may be interested in knowing that there are some unsolved problems here; see the article by Propp and Propp-Gubin for details.