Colouring identical cuboids

How many colours do we need to colour a fixed stack of identical cuboids with integer coordinates in such a way that no two cuboids of the same colour touch each other? The answer depends on the dimensions and orientations of the cuboids.

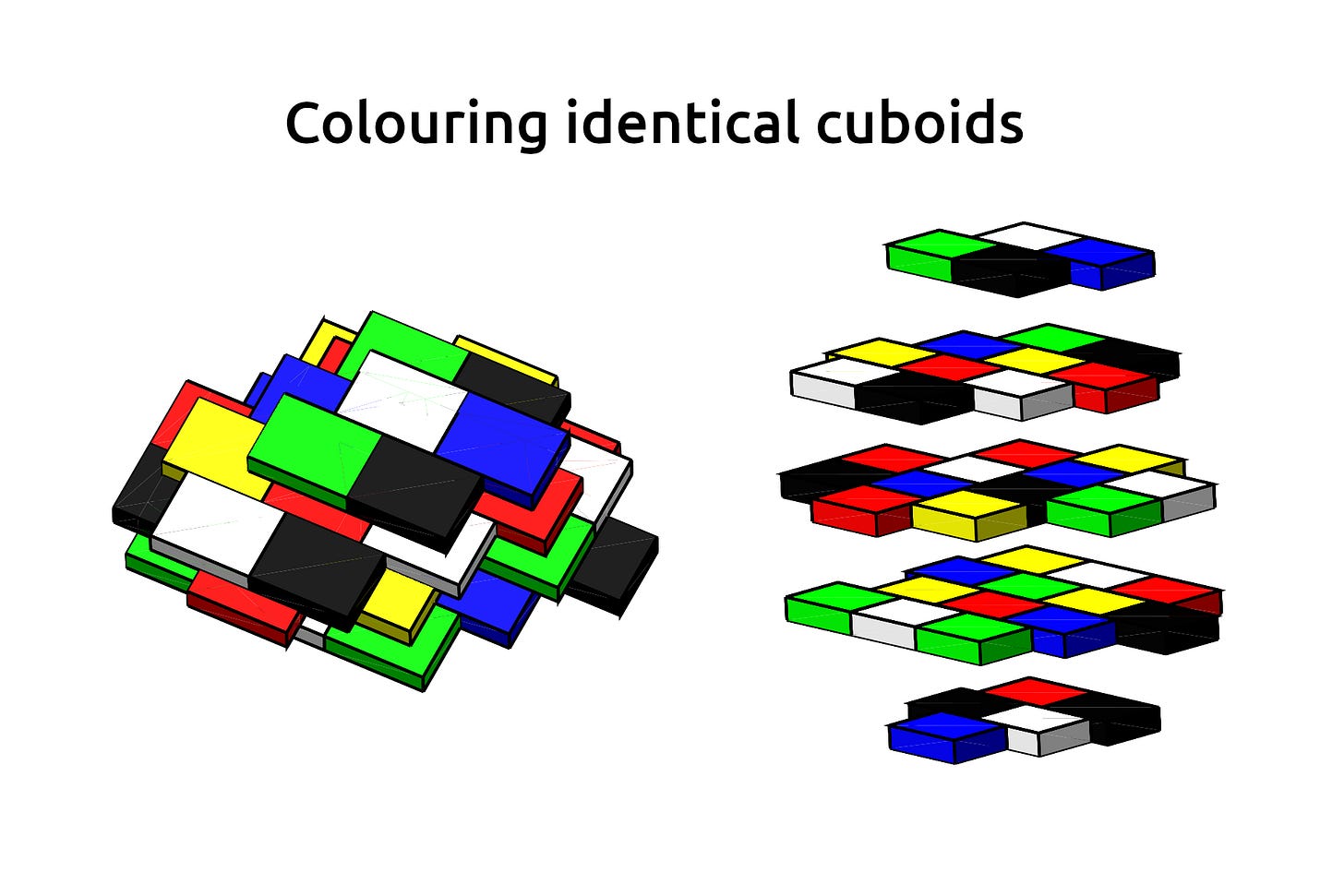
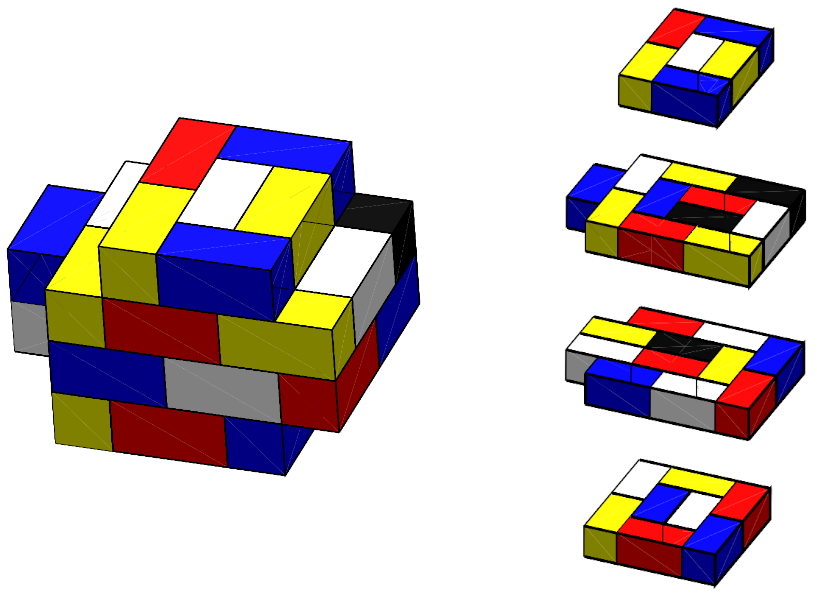
This problem is the subject of the recent paper Chromatic numbers for contact graphs of congruent cuboids by Søren Eilers, Rune Johansen, Rasmus Veber Rasmussen, and Carsten Thomassen. The authors prove that for 2×2×1 cuboids oriented in the same direction, the answer is five, and that the picture above gives an example of a stack where five colours are required.

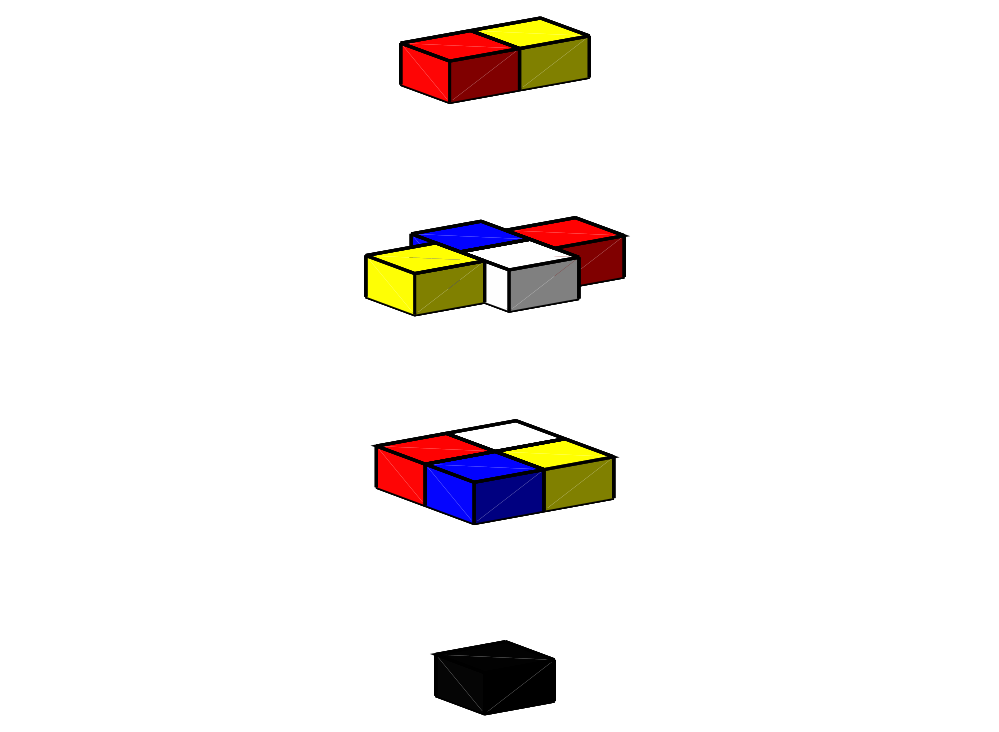
It is easier to see what is going on if the stack is decomposed into layers. One can check by inspection that no two cuboids of the same colour touch each other, but we also need to be sure that there is not a better way to colour the stack using only four colours, and this can be proved as follows. We first check that, up to permuting the colours, there is only one way to assign colours to the top two layers. This then forces the four cubes in the second to bottom layer to have four different colours, which in turn forces us to use a fifth colour for the cube in the bottom layer. The paper also proves the more difficult result that five colours suffice to colour any such stack of 2×2×1 cuboids.

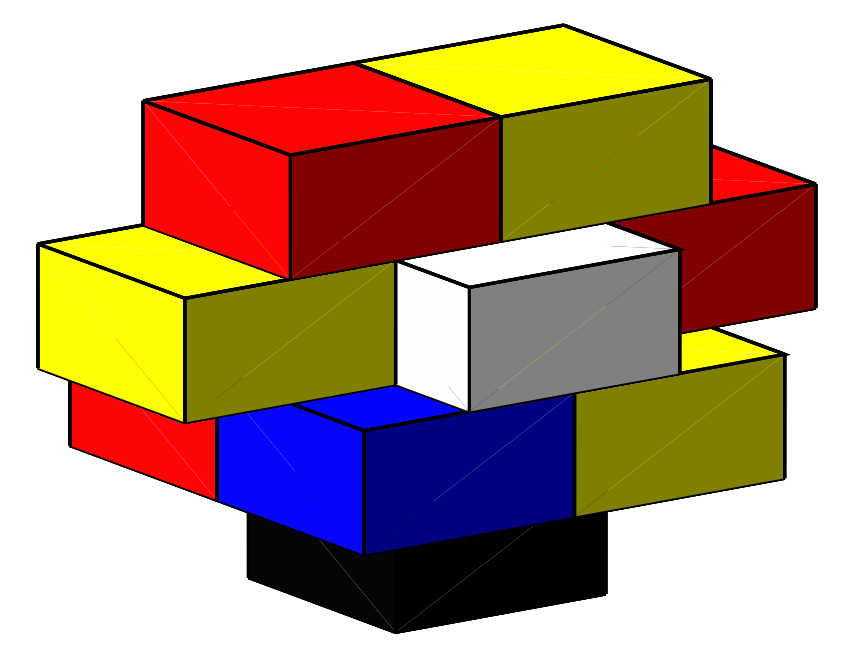
In the case of 3×1×1 cuboids that are oriented in the same direction, the authors prove that the answer is four, and that the picture above gives an example where four colours are required. A slightly more complicated argument can be used to prove that four colours are required to colour this particular example. Once again, proving that an arbitrary stack of 3×1×1 cuboids can be coloured with four colours is much harder, although the authors do prove this in the paper.

The authors use the notation χ₁(a,b,c) to denote the optimal number of colours needed to colour a stack of a×b×c cuboids that are all oriented in the same direction. The results of the previous two paragraphs can therefore be summarized by the statements χ₁(2,2,1)=5 and χ₁(3,1,1)=4. It is also relatively easy to prove that χ₁(2,1,1)=3.

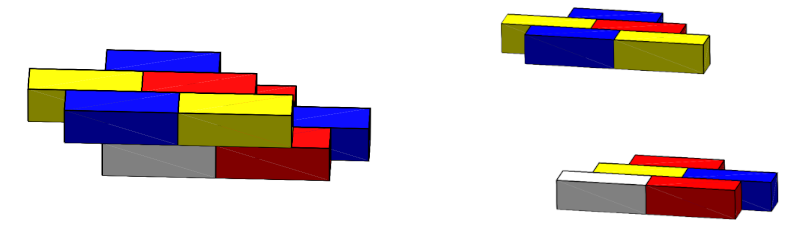
The paper uses the notation χ₂(a,b,c) to denote the optimal number of colours where the cuboids are all oriented in the same plane, but where they are allowed to lie at right angles to each other. The picture shows an example of such a configuration for 2×1×1 cuboids. The fact that χ₁(2,1,1)=3 immediately implies that χ₂(2,1,1) is at least 3, but the example in the picture above, which requires five colours, demonstrates that in fact χ₂(2,1,1) is at least 5. The authors also prove that χ₂(2,1,1) is exactly 5, meaning that five colours suffice for any such stack of 2×1×1 cuboids.

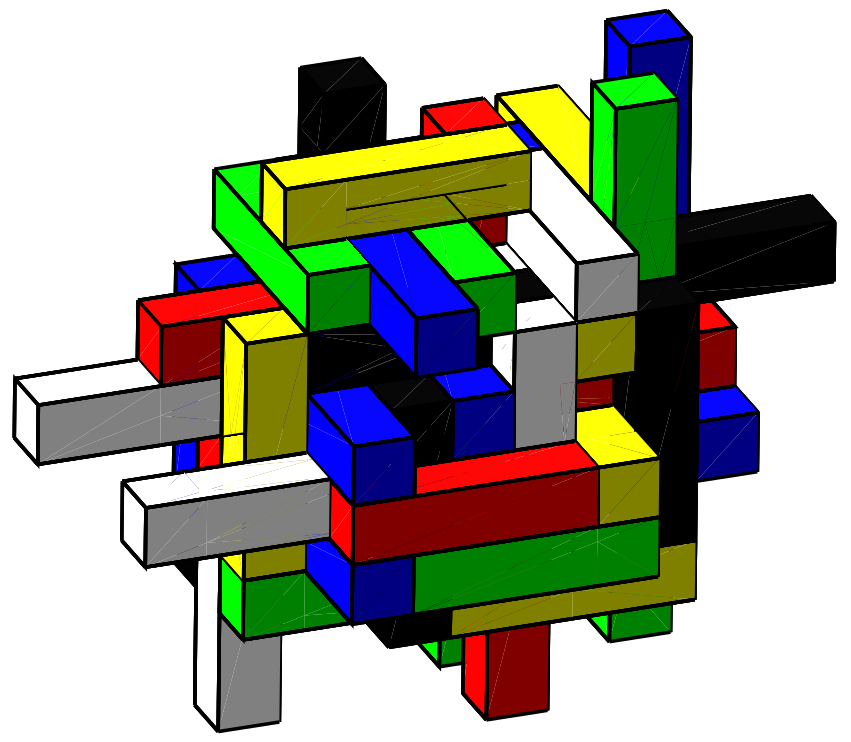
The paper takes things one step further and defines χ₃(a,b,c) as the optimal number of colours for a stack of a×b×c cuboids with arbitrary orientations. In this case, it is no longer possible to explode the arrangement into layers, which makes things harder to visualize and to communicate. The arrangement shown above, which consists of 56 cuboids of size 4×1×1, turns out to require six colours. This proves that χ₃(4,1,1) is at least 6. The paper establishes an upper bound of 12 for χ₃(4,1,1), but the exact value is not known.

It is possible to achieve a value of 6 even with cuboids having the same orientation. For example, the picture in the lead graphic gives an example demonstrating that χ₁(4,3,1) is at least 6. Despite extensive searches, the authors do not know of any example where seven colours are provably necessary, so it is conceivable that 6 is a universal upper bound for the problem. Even if this is the case, proving such a result sounds very difficult.

---

Picture credits and relevant links

All the graphics come from the paper by Søren Eilers, Rune Johansen, Rasmus Veber Rasmussen, and Carsten Thomassen.

These results are related to the Four Colour Theorem, which tells us that it is possible to colour any planar map with four colours in such a way that no two regions of the same colour touch each other. It follows from this that if a stack of cuboids can be exploded into layers, then at most four colours are needed to colour each layer in the stack.

Substack management by The Green Room.