Chess and the number e
The number e=2.718281828459045… is one of the most famous irrational numbers. It is most well known as the base of the natural logarithm, and is characterized by the fact that the derivative of ex is ex. What is less well known is that the number e also shows up in the solutions of discrete combinatorial problems, including problems related to chess.
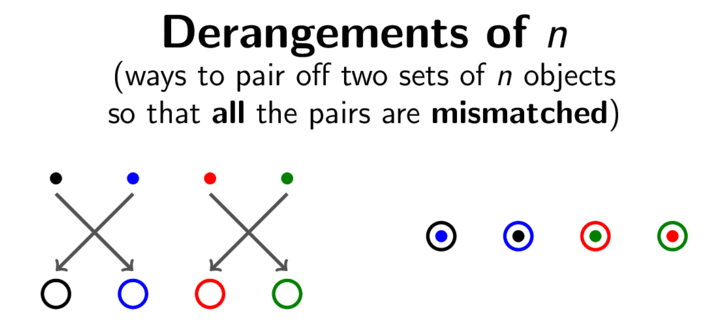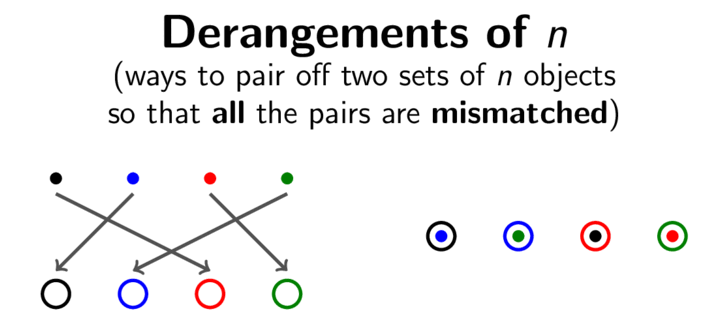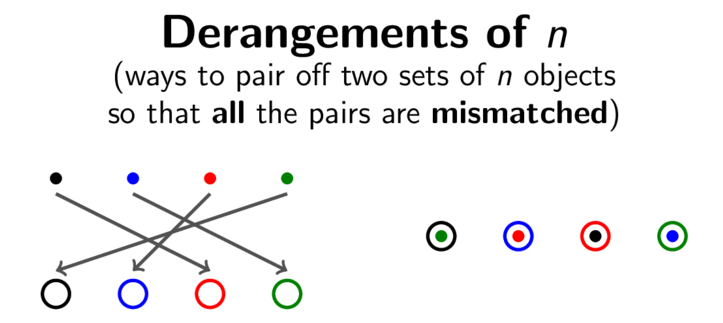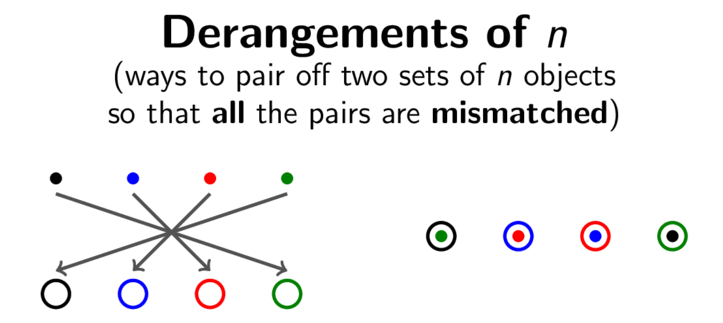
One surprising appearance of e is in the context of derangements. A derangement is a permutation of n objects with the property that each object is moved to a different one. Equivalently, imagine a situation in which a teacher randomly hands back n homework assignments to the n students who submitted them. A derangement corresponds to a situation in which every student receives the wrong assignment back. The animation above illustrates the homework assignment problem in the case n=4. In this case, the four coloured dots represent the four homework assignments, and the four coloured circles represent the corresponding students.
The formula for the number of derangements of n is shown above. In the case n=4, this works out as 24×(1 - 1 + ½ - ⅙ + 1/24), which is 9. You may recognize the formula as the power series expansion for n!/e, and indeed the formula converges to n!/e very quickly. For example, if n=11, then the number of permutations of 11 objects is 11 factorial, or 39,916,800, and the number of derangements is 14,684,570. Dividing the first number by the second gives 2.71828182842…, which agrees with e to 10 decimal places.
Another way to think about derangements is in terms of rooks on a chessboard. Mathematicians call an arrangement of rooks nonattacking if no two of the rooks are in the same row, and no two are in the same column. (This terminology is not entirely accurate, because it is not possible in chess for two pieces of the same colour to attack each other.) Two examples of nonattacking arrangements of rooks are shown in the picture below. The columns of the chessboard are labelled A to H from left to right, and the rows are labelled 1 to 8 from bottom to top.
This is a disguised version of the homework problem with 8 students, where the students are labelled A to H, the homework assignments are labelled 1 to 8, assignment 1 belongs to student A, assignment 2 belongs to student B, and so on. Both chess arrangements have a rook on A5, which corresponds to student A receiving assignment 5. However, the arrangement on the left does not correspond to a derangement, because, students B and G receive their own work back (B receives 2 and G receives 7). In contrast, the arrangement on the right is a derangement, as can be seen by the absence of a rook on the diagonal connecting A1 to H8.
It follows from this that if one randomly places 8 rooks on a standard chessboard in such a way that there is precisely one rook in each row and in each column, then the probability that there will be no rooks on the diagonal from A1 to H8 is approximately 1/e, or 36.8%. If we take n to be larger than 8, then the corresponding question for n rooks on an n by n board will lead to an even better approximation to e.
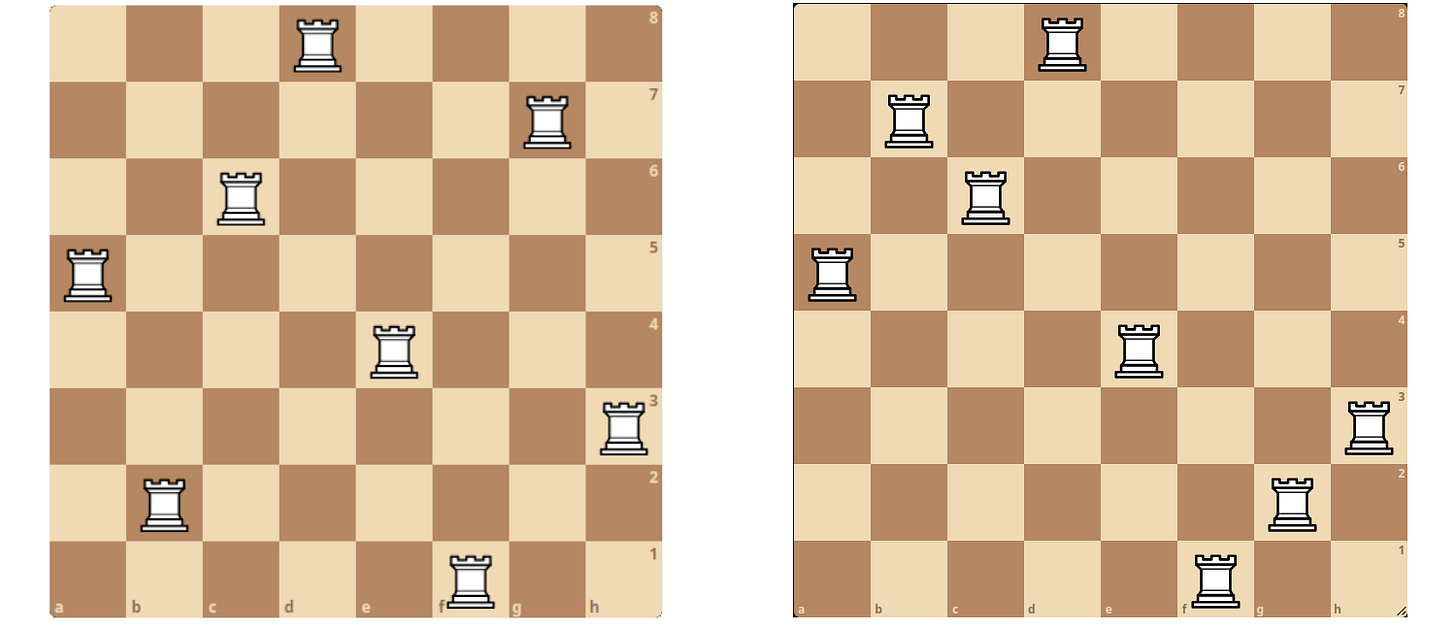
Now suppose that we place n rooks on an n by n board with no constraints, meaning that two rooks are allowed to be in the same row or column, so long as they are on different squares. A problem that is related to, but more difficult than the previous one is to determine the expected number of safe squares in this situation, meaning squares that are not attacked by any of the rooks. If there is a rook in each row and column, then there will be no safe squares. Other configurations may have many safe squares, such as the configuration of 8 rooks shown above, which has 25 safe squares, shown by the locations of the pawns. This problem was solved in the 2021 paper When Rooks Miss: Probability through Chess by Steven J. Miller, Haoyu Sheng, and Daniel Turek. The answer turns out to be that the expected number of safe squares is n2/e2. In other words, the probability that a random square will be safe in a random configuration of n rooks converges to 1/e2 (about 13.5%) as n tends to infinity.
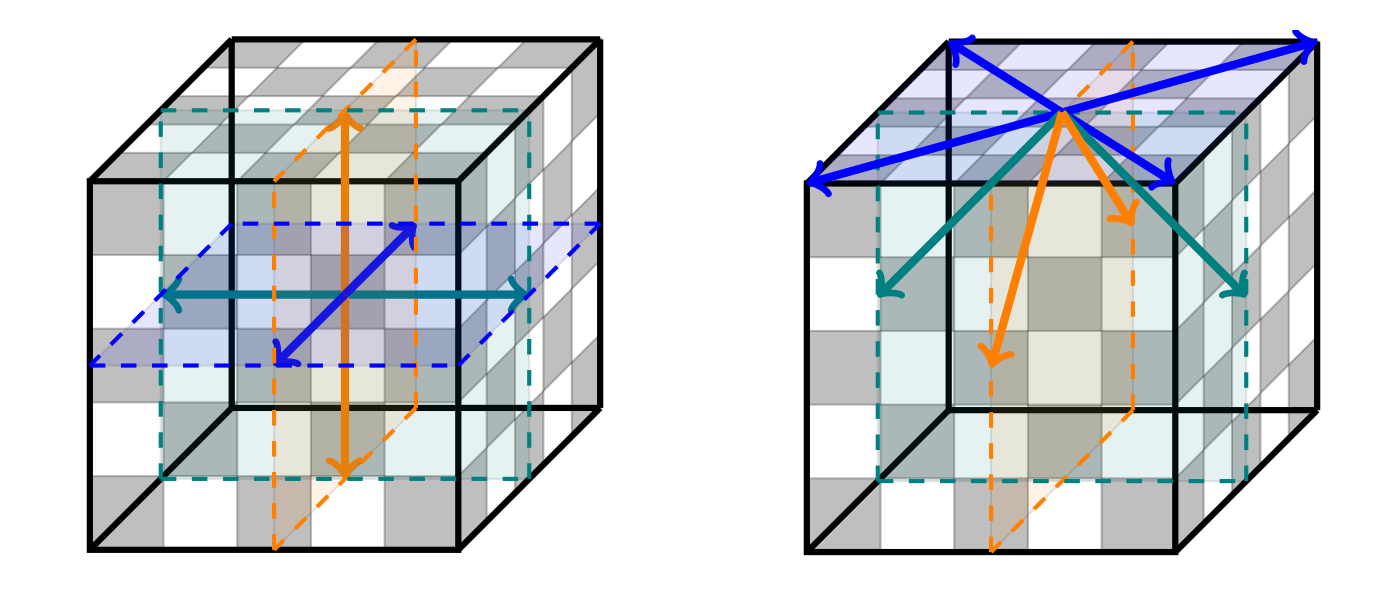
The recent paper Hyper-bishops, Hyper-rooks, and Hyper-queens: Percentage of Safe Squares on Higher Dimensional Chess Boards by Caroline Cashman, Joseph Cooper, Raul Marquez, Steven J. Miller, and Jenna Shuffelton gives many generalizations of the safe squares problem for rooks. In particular, the authors solve the corresponding problem for bishops and for queens. The analysis is made more difficult by the fact that a rook attacks the same number of squares no matter where it is placed on the board, whereas this is not the case for bishops or queens. Despite this complication, the conclusion is similar to the conclusion for the rook problem: the proportion of safe squares for n randomly placed pieces on an n by n chess board converges to 2/e2 if the pieces are bishops, and 2/e4 if the pieces are queens. The paper also studies a variety of k-dimensional versions of the problem involving generalized pieces such as “line rooks” and “line bishops”, which move according to the rules shown above.
Picture credits and relevant links
The illustrations of the moves of the line rook and line bishop come from the paper by Caroline Cashman, Joseph Cooper, Raul Marquez, Steven J. Miller, and Jenna Shuffelton.
The other graphics are my own work, using the tools at lichess.org.
Wikipedia has a page about derangements.
Substack management by Buzz & Hum.
We have just launched a companion website to this Substack, which you can find at apieceofthepi.com.





From the work of Peter Cameron, would random latin squares be useful in the analysis of safe squares?
As usual, your discussion of the relation of mathematics to a game (in this case chess) is excellent. These concrete examples really help understand the mathematical analyses.