Balanced Steinhaus triangles

A familiar fact from the game of pool is that 15 objects can be arranged in an equilateral triangle of side length 5. This is because 15=1+2+3+4+5 is the fifth triangular number, T(5), where T(n)= n(n+1)/2. If we have balls of five different colours, it is possible to create an arrangement like this where there are equally many balls of each colour, for the simple reason that 15 is a multiple of 5. In the context of pool, it is important that it is not possible to do this with only two colours, such as red and yellow.

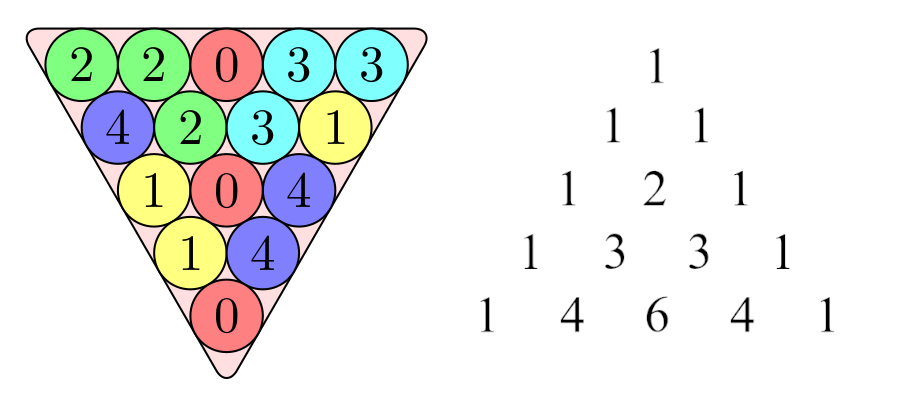
Now suppose that we have an equilateral triangle of side length n that is packed with a collection of balls of m different colours, numbered 0, 1, 2, up to m–1. An arrangement like this is called a Steinhaus triangle if each entry is the sum of the two adjacent entries in the row above, where entries are read modulo m. The picture above shows a Steinhaus triangle where n and m are both equal to 5. For example, the two 2s in the top row add up to the 4 in the second row, and the 4 and the 2 in the second row add up to the 1 in the third row, because 1 is congruent to 4+2=6 modulo 5. This rule is similar to the rule for generating Pascal’s triangle (shown above and to the right). It follows from the definition that a Steinhaus triangle is completely determined by its top row. The Steinhaus triangle shown above has the additional property of being balanced, which means that there are equally many balls of each colour.

Steinhaus triangles are named after Hugo Steinhaus, who introduced them (in the case m=2) in 1964. The picture above, which somewhat resembles the Sierpiński triangle fractal, shows a Steinhaus triangle with parameters m=2 and n=24. The triangle is balanced, and consists of 150 red balls (representing 0 modulo 2) and 150 blue balls (representing 1 modulo 2).

A natural question to ask is: given two integers m and n, when is it possible to construct a balanced Steinhaus triangle with these parameters? One necessary condition is that the n-th triangle number, T(n), must be a multiple of m, just as 15 is a multiple of 5. In 1978, John C. Molluzzo asked whether the converse is true: if T(n) is a multiple of m, does this guarantee the existence of a balanced Steinhaus triangle with parameters m and n? The answer is “yes” for m=2, 3, 5, or 7, but “no” in general. For example there is no balanced Steinhaus triangle with parameters m=15 and n=5, or m=21 and n=6, even though T(n) is a multiple of m in each case.

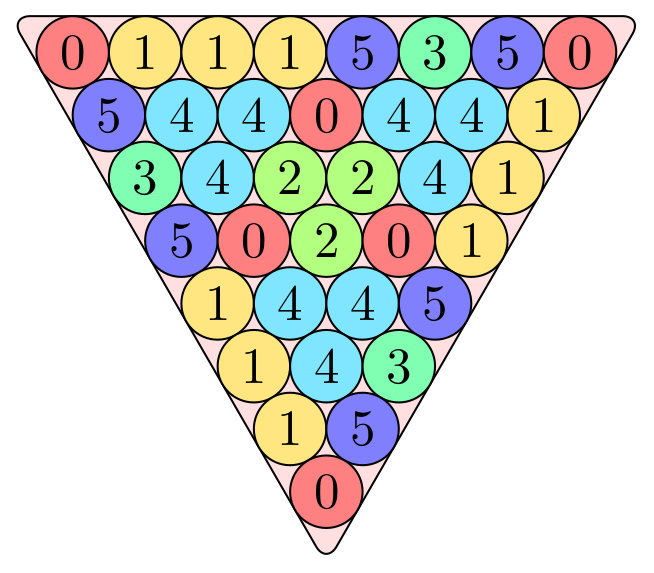
There is a second type of Steinhaus triangle, such as the one shown above, in which each entry is equal to the negative of the sum of the two entries above it. In this example, we have m=6 and n=8, so the entries of the triangle are integers modulo 6. The 0 and 1 in the first row are above a 5 in the second row, because 0+1+5 is a multiple of 6. Similarly, the 4 and 5 in the fifth row are above a 3 in the sixth row, because 4+5+3 is a multiple of 6. One advantage of this rule is that it is invariant under rotations and reflections. In fact, although this particular Steinhaus triangle is not balanced, it remains the same after it is rotated by 120°.

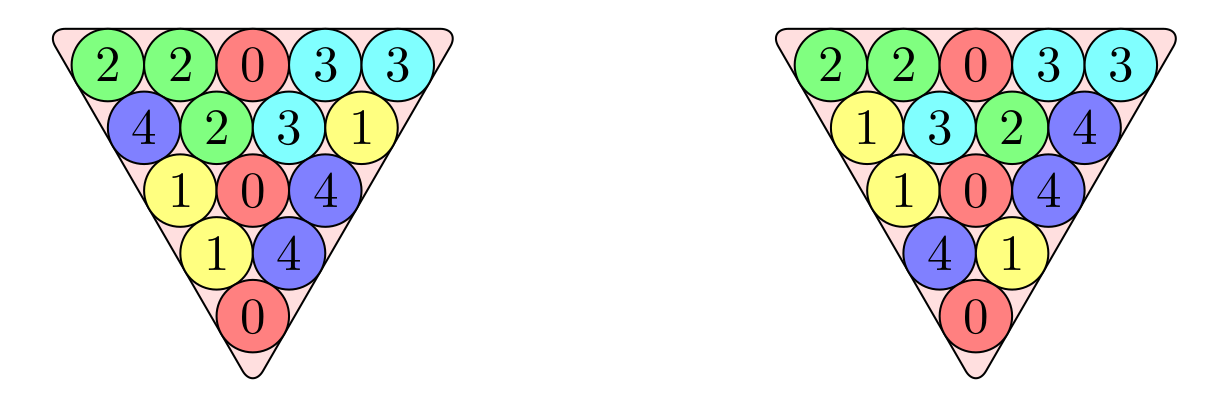
It is also possible to have balanced Steinhaus triangles of the second type. The picture above shows two balanced Steinhaus triangles with m=n=5. The one on the left follows the first rule, where each entry is the sum of the two above it, and the one on the right follows the second rule, where the sum of each entry and the two above it is a multiple of m, or 5 in this case. These triangles are closely related to each other: the triangle on the right can be obtained from the triangle on the left by reversing the order of the entries in the second row and in the fourth row. This happens because the first row of the triangle (2, 2, 0, 3, 3) is antisymmetric, which means that its negation, (-2, -2, 0, -3, -3), is congruent modulo 5 to its reversal, (3, 3, 0, 2, 2).

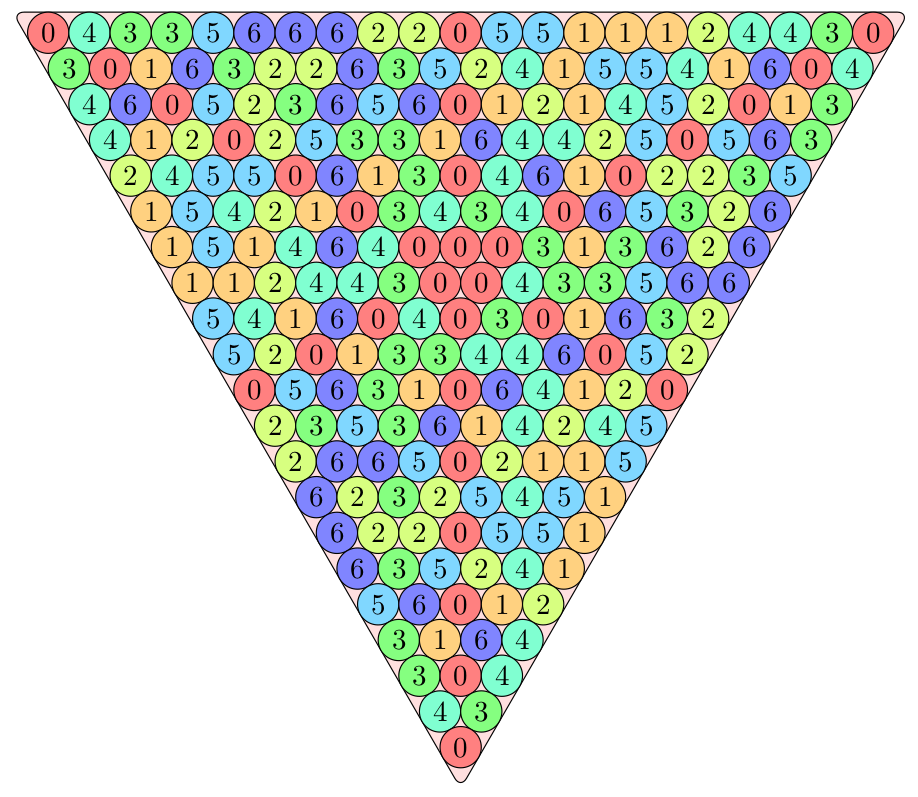
I found out about Steinhaus triangles from the recent paper Balanced Steinhaus triangles by Jonathan Chappelon. The paper is over 100 pages long and contains many beautiful diagrams, such as the one above, which shows a balanced Steinhaus triangle with m=7 and n=21 that has been constructed using the second rule. The paper gives a positive answer to a weaker version of Molluzzo’s original question, proving that for any fixed value of m, there are infinitely many balanced Steinhaus triangles modulo m. Another way to say this is that for any fixed value of m, there are arbitrarily large balanced Steinhaus triangles modulo m.

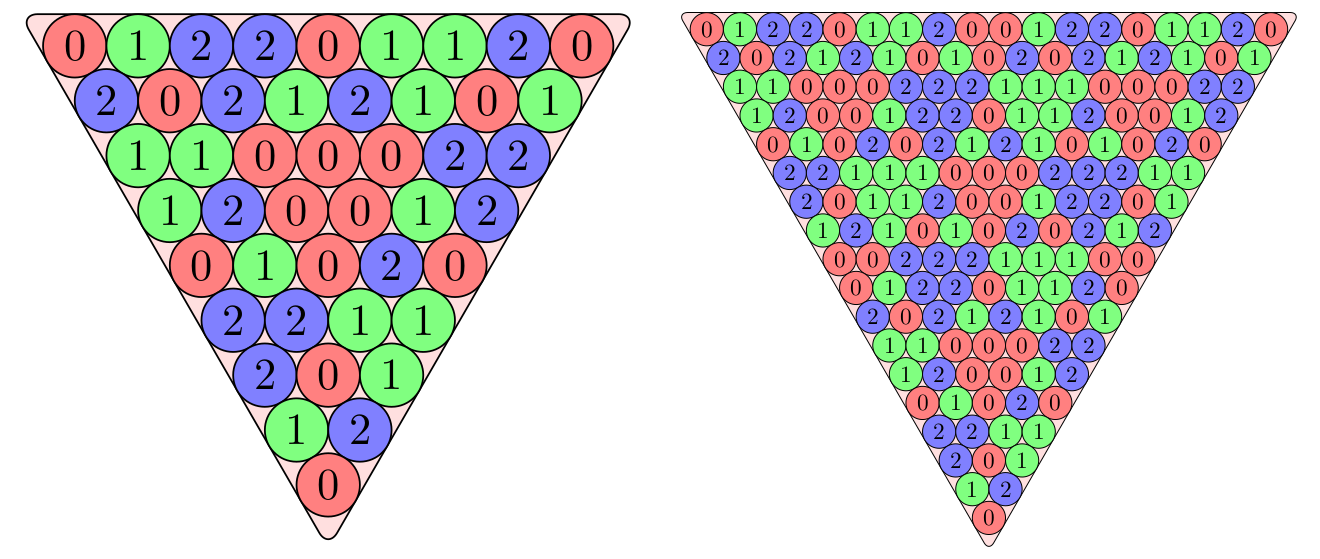
The triangles are constructed by starting with an antisymmetric sequence, in this case (0, 1, 2, 2, 0, 1, 1, 2, 0) modulo 3, and using it as the top row of a balanced Steinhaus triangle of the second type, such as the one above and to the left, which has parameters m=3 and n=9. This sequence has the remarkable property that simply by repeating it over and over, it is possible to construct larger and larger balanced Steinhaus triangles. For example, repeating the previous sequence twice in succession gives the top row of the balanced Steinhaus triangle with m=3 and n=9×2=18 shown above and to the right. The difficult part of the paper is proving the existence of an antisymmetric sequence with the correct property.

The paper also gives pictures of balanced Steinhaus triples with large numbers of dots, such as the one above, which has parameters m=9 and n=54, and 165 dots of each colour. This reminds me of the pattern of dots on a colour TV screen from the 1970s.

---

Picture credits and relevant links

The picture of the pool balls is by SouthcottC and the diagram of Pascal’s triangle is by Svjo. Both pictures appear on Wikimedia Commons.

The other pictures come from the paper by Jonathan Chappelon.

Wikipedia has a page on Hugo Steinhaus (1887–1972).