Anti-inductive dice

David and Goliath each have a six-sided die. David’s die has the numbers {1, 1, 4, 4, 5, 6}, and Goliath’s die has the numbers {0, 1, 2, 6, 6, 6}. If each of them throws his die n times and announces the total, then Goliath is more likely than David to have the higher total, except when n=4. This surprising phenomenon is discussed in the recent paper The Paradox of Anti-Inductive Dice by Summer Eldridge, Ivo David de Oliveira, and Yogev Shpilman.

A more familiar paradoxical type of dice are intransitive dice. The word transitive describes a relation such as the “greater than” relation on numbers. It refers to the property that whenever A > B and B > C hold, it must also be the case that A > C, which intuitively means that if A beats B and B beats C, then A must beat C. In contrast, the “beats” relation on the set {rock, paper, scissors} is not transitive: scissors beat paper and paper beats rock, but scissors do not beat rock. In the case of “rock, paper, scissors”, the intransitive property is what makes the game useful for resolving deadlocks.

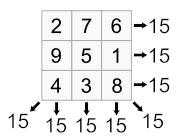
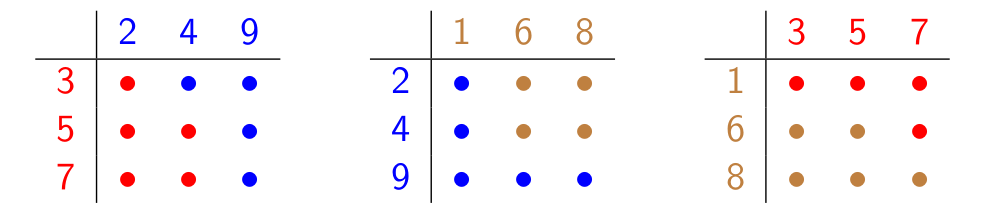
Intransitive dice are dice that exhibit “rock, paper, scissors” type behaviour. It turns out that we can construct a simple example of three intransitive dice using the three columns of the 3 by 3 magic square shown above, which has the property that each row, each column, and each long diagonal adds up to 15. This produces three dice: a blue die A with labels {2, 4, 9}, a red die B with labels {3, 5, 7}, and a gold die C with labels {1, 6, 8}. It is admittedly somewhat hard to imagine a three-sided die, but it is possible to simulate one by taking a standard six-sided die and using each label twice. The “intransitive” property of these dice, as shown in the table below, is that A loses to B most of the time, and B loses to C most of the time, and yet C also loses to A most of the time. (In each case, “most of the time” means “5 times out of every 9”.)

The word “anti-inductive” in the David and Goliath example mentioned earlier is a reference to the principle of mathematical induction. This is a proof technique that is based on the idea that if we know that a property P(n) holds whenever n is one of the integers 1, 2, 3, up to k, then we may be able to prove that P(n) also holds when n=k+1. Let us take P(n) to be the claim that “if David and Goliath each throws his die n times, then Goliath is more likely than David to have a higher total”. In particular, P(1) is the claim that if David and Goliath each throws his die once, then Goliath is more likely than David is to win.

The table above shows the 36 possible outcomes if David and Goliath each throws his die once: Goliath wins in 17 cases, David wins in 14 cases, and the outcome is a tie in the other 5 cases. Goliath thus has a better chance of winning than David does, which proves that P(1) is true. A more detailed analysis shows that P(2) and P(3) are also true statements, but P(4) is not: after four iterations of the game, David has a better chance of winning than Goliath does. The real surprise is that for larger values of n, the situation reverses again, and Goliath has a better chance of winning the game for all n greater than or equal to 5. Having said that, the winning margins are very slim, and each player will have a total score very close to 3.5n if n is very large and the dice are fair.

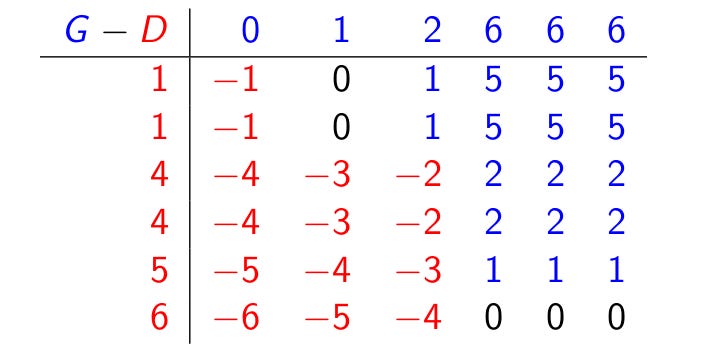
We can also model the David versus Goliath dice game in terms of a hypothetical 36-sided die, each of whose faces is the value of Goliath’s die minus the value of David’s die, as shown in the table above. The situations where Goliath wins correspond to the situations where the 36-sided die shows a positive value, meaning that the hypothetical 36-sided die would beat the die with zeros on every face.

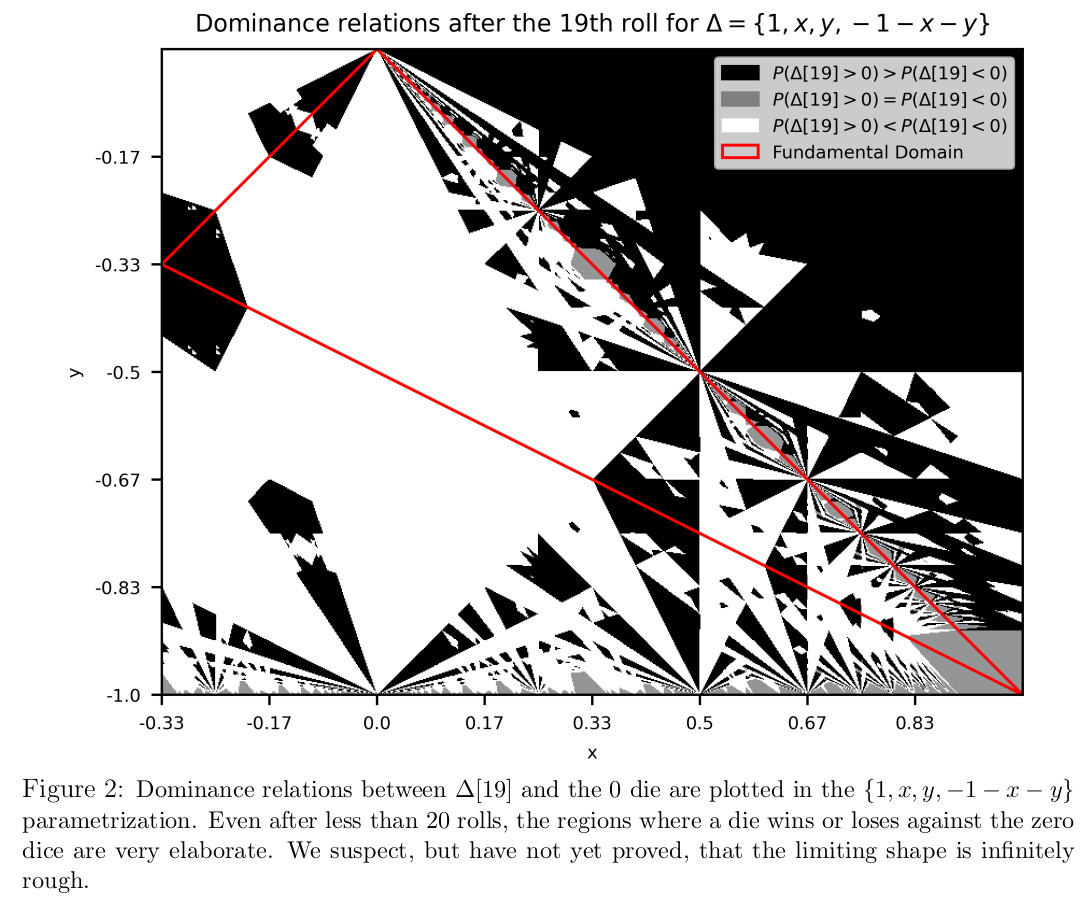
The paper by Eldridge, de Oliveira, and Shpilman also studies the case of four-sided dice in some depth. Up to normalization and symmetries, they show how it is possible to identify such dice with points in a triangular region of two-dimensional space. The picture above describes what happens after a die is thrown 19 times. A point is coloured white if a die corresponding to it usually loses to the zero die, black if it usually beats the zero die, and grey if it wins exactly half the time against the zero die. Remarkably, the set of possible outcomes exhibits very intricate behaviour, and arbitrarily small changes in the input parameters can make the difference between a die winning or losing after 19 throws.

---

Picture credits and relevant links

The magic square graphic is by Phidauex and appears on Wikipedia.

The fractal-like picture comes from the paper by Summer Eldridge, Ivo David de Oliveira, and Yogev Shpilman.

The David and Goliath picture is an edited version of an image I created with OpenAI’s tool Sora.

The other graphics are my own work.

Substack management by Buzz & Hum.